题目内容
已知函数f(x)=log2(2x+1-2t)的值域为R,则实数t的取值范围是 .
考点:对数函数图象与性质的综合应用,复合函数的单调性
专题:函数的性质及应用
分析:令g(x)=2x+1-2t,由题意函数的值域为R,则可得g(x)可以取所有的正数可得,即函数g(x)=2x+1-2t的值域B满足:(0,+∞)⊆B,由此构造关于t的不等式,解不等式可求.
解答:
解:令g(x)=2x+1-2t
由题意函数的值域为R,则可得g(x)可以取所有的正数
令函数g(x)=2x+1-2t的值域B,则(0,+∞)⊆B
∵B=(1-2t,+∞)
∴1-2t≤0
解得t≥
,
故实数t的取值范围是[
,+∞)
故答案为:[
,+∞)
由题意函数的值域为R,则可得g(x)可以取所有的正数
令函数g(x)=2x+1-2t的值域B,则(0,+∞)⊆B
∵B=(1-2t,+∞)
∴1-2t≤0
解得t≥
| 1 |
| 2 |
故实数t的取值范围是[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题主要考查了由指数函数与对数函数复合的复合函数,解题的关键是要熟悉对数函数的性质,解题时要注意区别与函数的定义域为R的限制条件.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
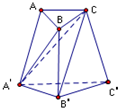 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
已知曲线C:x2+y2-2x+2y=0与直线L:y+2=k(x-2),则C与L的公共点( )
| A、有2个 | B、最多1个 |
| C、至少1个 | D、不存在 |
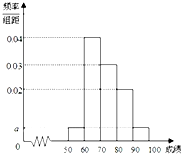 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].