题目内容
各棱均为2的正四棱锥的内切球的半径为 .
考点:球内接多面体
专题:计算题
分析:求出正四棱锥的体积,然后求出正四棱锥的表面积,利用等体积方法求解即可.
解答:
解:如图,设正四棱锥底面的中心为O,则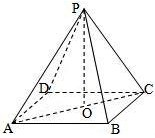
在直角三角形ABC中,AC=2
,
∴AO=CO=
,
在直角三角形PAO中,PO=
,
∴正四棱锥的体积为:
×4×
,
而正四棱锥内切球的半径为r,
正四棱锥的表面积为:4+4×
×22,
正四棱锥的体积:
S表面积•r,
∴
(4+4×
×22)r=
×4×
,
球的半径r=
,
故答案为:
.

在直角三角形ABC中,AC=2
| 2 |
∴AO=CO=
| 2 |
在直角三角形PAO中,PO=
| 2 |
∴正四棱锥的体积为:
| 1 |
| 3 |
| 2 |
而正四棱锥内切球的半径为r,
正四棱锥的表面积为:4+4×
| ||
| 4 |
正四棱锥的体积:
| 1 |
| 3 |
∴
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| 2 |
球的半径r=
| ||||
| 2 |
故答案为:
| ||||
| 2 |
点评:本题主要考查球的体积,球的外接体问题,考查计算能力和空间想象能力,等体积方法求出球的半径是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
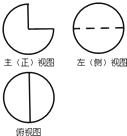

| A、16π | B、14π |
| C、12π | D、8π |
在区间[0,1]上随机取三个数x,y,z,事件A={(x,y,z)|x2+y2+z2<1},则P(A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
下列函数中,在区间(0,2)上单调递减的是( )
A、y=-
| |||
| B、y=lnx | |||
C、y=-
| |||
| D、y=|x| |
若log4x=1,则
的值为( )
| x |
| A、2 | B、±2 | C、0 | D、4 |