Question

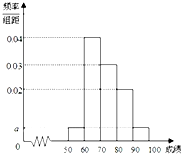某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）图中语文成绩的众数是

 

；
（2）图中a=

 

；
（3）若80分以上为优秀，则语文成绩有

 

个人优秀；
（4）根据频率分布直方图，估计这100名学生语文成绩的平均分解．

Answer 1

考点：频率分布直方图,众数、中位数、平均数

专题：概率与统计

分析：（1）利用众数的意义即可得出；
（2）根据频率分布直方图中各小矩形面积之和等于1即可得出；
（3）根据80分以上的频率，即可得到频数；
（4）根据平均数的意义即可得出．

解答： 解：（1）众数是65．  
（2）依题意得，10（2a+0.02+0.03+0.04）=1，解得a=0.005． 
（3）若80分以上为优秀，则由图知80分以上的频率为：10×0.02+10×0.005=0.25
则语文成绩有100×0.25=25个人优秀．
（4）这100名学生语文成绩的平均分为：55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73（分）． 
故答案为：：（1）65；（2）0.005；（3）25；（4）73．

点评：熟练掌握利用频率分布直方图求众数、平均数、中位数及知道频率分布直方图中各小矩形面积之和等于1等性质是解题的关键．