题目内容
正四面体棱长为a,求其内切球与外接球的表面积.
考点:球内接多面体
专题:计算题,球
分析:由正四面体的棱长,求出正四面体的高,设外接球半径为R,利用三角形相似求出R的值r的值,可求外接球的表面积以及内切球的表面积.
解答:
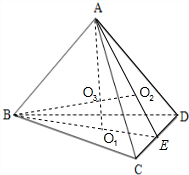 解:设正四面体的面BCD和面ACD的中心分别为O1,O2,连结AO2与BO1并延长,必交于CD的中点E,
解:设正四面体的面BCD和面ACD的中心分别为O1,O2,连结AO2与BO1并延长,必交于CD的中点E,
又BE=
a,O2E=
a,连接BO2,在Rt△BO2E中,BO2=
,连结AO1与BO2交于O3,
由Rt△AO2O3≌Rt△BO1O2,
∴O3O2=O3O1,O3A=O3B,
同理可证O3C=O3D=O3A,O3到另二面的距离也等O3O1,
∴O3为四面体外接球与内接球的球心,由△BO1O3∽△BO2E,
∴O1O3=
a,
∴R外=
a,S外=
πa2,r内=
a,S内=
πa2.
 解:设正四面体的面BCD和面ACD的中心分别为O1,O2,连结AO2与BO1并延长,必交于CD的中点E,
解:设正四面体的面BCD和面ACD的中心分别为O1,O2,连结AO2与BO1并延长,必交于CD的中点E,又BE=
| ||
| 2 |
| ||
| 6 |
| ||
| 3 |
由Rt△AO2O3≌Rt△BO1O2,
∴O3O2=O3O1,O3A=O3B,
同理可证O3C=O3D=O3A,O3到另二面的距离也等O3O1,
∴O3为四面体外接球与内接球的球心,由△BO1O3∽△BO2E,
∴O1O3=
| ||
| 12 |
∴R外=
| ||
| 4 |
| 3 |
| 2 |
| ||
| 12 |
| 1 |
| 6 |
点评:本题考查球的内接多面体的知识,考查计算能力,逻辑思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
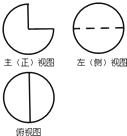

| A、16π | B、14π |
| C、12π | D、8π |
在区间[0,1]上随机取三个数x,y,z,事件A={(x,y,z)|x2+y2+z2<1},则P(A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
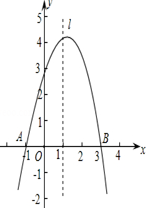 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.