题目内容
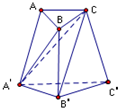 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
考点:组合几何体的面积、体积问题
专题:计算题
分析:利用棱台的底面相似,通过相似比求出几何体的体积比,推出结果即可.
解答:
解:因为几何体是三棱台,所以两个底面相似,∵AB:A′B′=1:2,
∴SA′B′C′:SABC=1:4,设棱台的高为h,
∴
=
=1:4.
∴三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为4:2:1.
故选:C.
∴SA′B′C′:SABC=1:4,设棱台的高为h,
∴
| VC-A′B′C′ |
| VA′-ABC |
| ||
|
∴三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为4:2:1.
故选:C.
点评:本题考查几何体的体积的比的求法,注意体积比与相似比关系的应用,考查计算能力.

练习册系列答案
相关题目
在区间[0,1]上随机取三个数x,y,z,事件A={(x,y,z)|x2+y2+z2<1},则P(A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
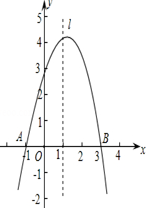 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.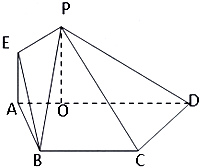 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,