题目内容
咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
考点:简单线性规划的应用
专题:计算题,数形结合
分析:首先设咖啡馆每天配制甲种饮料x杯,乙种饮料y杯,获利z元.建立目标函数z=0.7x+1.2y,求出x,y的线性约束条件,画出可行域,找到最优解.按照这样的步骤求解即可.
解答:
解:设咖啡馆每天配制甲种饮料x杯,乙种饮料y杯,获利z元.
则z=0.7x+1.2y
约束条件为:
…(6分)

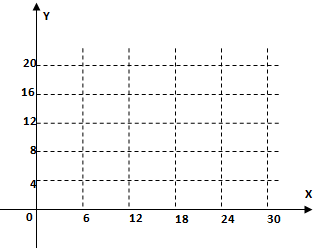
如图所示,在点C(200,240)处,即x=200,y=240时zmax=428(元)…(12分)
答:咖啡馆每天配制甲种饮料200杯,乙种饮料240杯,能使咖啡馆获利最大.
则z=0.7x+1.2y
约束条件为:
|

如图所示,在点C(200,240)处,即x=200,y=240时zmax=428(元)…(12分)
答:咖啡馆每天配制甲种饮料200杯,乙种饮料240杯,能使咖啡馆获利最大.
点评:本题属于线性规则的题目.考查线性规划的应用,正确列出约束条件画出可行域是解题的关键.

练习册系列答案
相关题目
已知圆锥的底面半径为R,高为H,则圆锥内接圆柱体的体积最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
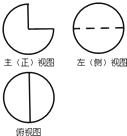

| A、16π | B、14π |
| C、12π | D、8π |