题目内容
在椭圆C:
+
=
中,当离心率e趋近于0,椭圆就趋近于圆,类比圆的面积公式,椭圆C的面积S椭圆= .
| x2 |
| a2 |
| y2 |
| b2 |
|
考点:类比推理
专题:推理和证明
分析:半径为r的圆的面积公式为πr2=π•r•r,利用类比推理,可得椭圆C的面积.
解答:
解:半径为r的圆的面积公式为πr2=π•r•r,在椭圆C:
+
=
中,当离心率e趋近于0,椭圆就趋近于圆,a,b无限接近圆的半径r,
∴椭圆C的面积S椭圆=πab.
故答案为:πab.
| x2 |
| a2 |
| y2 |
| b2 |
|
∴椭圆C的面积S椭圆=πab.
故答案为:πab.
点评:本题考查类比推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积的和的
,且样本容量为200,则中间一组有频数为( )
| 1 |
| 4 |
| A、40 | B、32 |
| C、0.2 | D、0.25 |
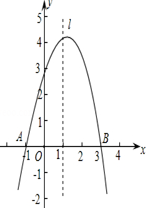 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.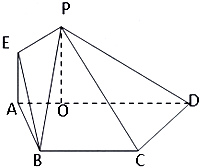 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,