题目内容
已知函数f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值1,那么此函数在[-2,2]上的最小值是( )
| A、-39 | B、-31 |
| C、-7 | D、以上都不对 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,导数的综合应用
分析:求导f′(x)=6x2-12x=6x(x-2),从而可得f(x)在[-2,0]上是增函数,在[0,2]上是减函数;从而可得函数的最小值.
解答:
解:∵f(x)=2x3-6x2+m,
∴f′(x)=6x2-12x=6x(x-2),
∴当x>2或x<0时,f′(x)>0;
当0<x<2时,f′(x)<0;
故f(x)在[-2,0]上是增函数,在[0,2]上是减函数;
故f(0)=0+m=1;
故m=1;
而f(-2)=-16-24+1=-39,
f(2)=16-24+1=-7;
故fmin(x)=f(-2)=-39;
故选A.
∴f′(x)=6x2-12x=6x(x-2),
∴当x>2或x<0时,f′(x)>0;
当0<x<2时,f′(x)<0;
故f(x)在[-2,0]上是增函数,在[0,2]上是减函数;
故f(0)=0+m=1;
故m=1;
而f(-2)=-16-24+1=-39,
f(2)=16-24+1=-7;
故fmin(x)=f(-2)=-39;
故选A.
点评:本题考查了导数的综合应用及导数的判断与应用,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
函数f(x)=lgx-
的零点所在的区间为( )
| 1 |
| x |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体得三视图如图所示,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、5
|
已知平面向量
与
的夹角为
,且|
|=1,|
+2
|=2
,则|
|=( )
| a |
| b |
| π |
| 3 |
| b |
| a |
| b |
| 3 |
| a |
| A、1 | ||
B、
| ||
| C、3 | ||
| D、2 |
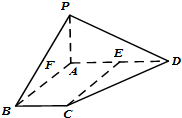 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=