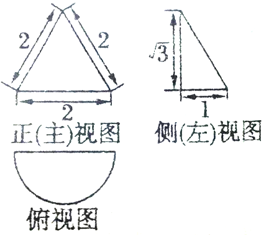
题目内容
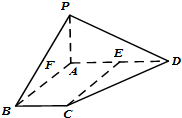 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=| 1 |
| 2 |
| PF |
| PB |
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)设二面角F-CD-E的平面角为θ,当tanθ=
| 1 |
| 2 |
考点:用空间向量求平面间的夹角,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得四边形AEBC为平行四边形,AB∥CE,由此能证明CE∥平面PAB.
(Ⅱ)法一:过F作FH∥AP交AB于点H,由已知得FH⊥平面ABCD,过H作HG⊥CD交直线CD于点G,连接FG,则∠FGH即为二面角F-CD-E的平面角,延长AB与DC交于点Q,设FH=a,则HG=2a,由此能求出λ=
=
=
=
.
(Ⅱ)法二:以A为坐标原点如图建立空间直角坐标系,利用向量法能求出λ=
.
(Ⅱ)法一:过F作FH∥AP交AB于点H,由已知得FH⊥平面ABCD,过H作HG⊥CD交直线CD于点G,连接FG,则∠FGH即为二面角F-CD-E的平面角,延长AB与DC交于点Q,设FH=a,则HG=2a,由此能求出λ=
| PF |
| PB |
| AH |
| AB |
| 2a |
| 3a |
| 2 |
| 3 |
(Ⅱ)法二:以A为坐标原点如图建立空间直角坐标系,利用向量法能求出λ=
| 2 |
| 3 |
解答:
解:(Ⅰ)证明:∵E为AD的中点,BC=
AD,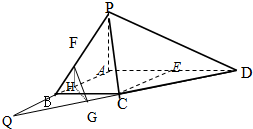
∴AE=BC,又AD∥BC,∴四边形AEBC为平行四边形,AB∥CE,
又CE?平面PAB,AB?平面PAB,
∴CE∥平面PAB.
(Ⅱ)解法一:过F作FH∥AP交AB于点H,
∵PA⊥平面ABCD,∴FH⊥平面ABCD,
过H作HG⊥CD交直线CD于点G,连接FG,则FG⊥CD,
∴∠FGH即为二面角F-CD-E的平面角,tan∠FGH=
,
延长AB与DC交于点Q,设FH=a,则HG=2a,
又∵PA=AB=BC=
AD,∴∠BQC=30°,∠PBA=45°,
在Rt△HGQ中,HQ=4a,Rt△PHB中,BH=FH=a,则 BQ=3a,HA=2a,
∴λ=
=
=
=
.
(Ⅱ)解法二:以A为坐标原点如图建立空间直角坐标系,
设AB=1,则B(1,0,0) ,C(
,
,0) ,D(-1,
,0)
由λ=
,得
=λ
,λ∈(0,1)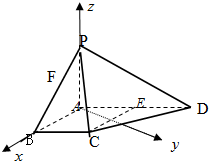 ,由已知得F(λ,0,1-λ)
,由已知得F(λ,0,1-λ)
则
=(λ-
,-
,1-λ),
=(λ+1,-
,1-λ),
设平面FCD的法向量
=(1,y,z),
由
,得
=(1,
,
),
又平面CDE的法向量为
1=(0,0,1),
由tanθ=
,得cosθ=
,
由cosθ=
=
,
解得λ=
或λ=
(舍去),所以λ=
.
| 1 |
| 2 |

∴AE=BC,又AD∥BC,∴四边形AEBC为平行四边形,AB∥CE,
又CE?平面PAB,AB?平面PAB,
∴CE∥平面PAB.
(Ⅱ)解法一:过F作FH∥AP交AB于点H,
∵PA⊥平面ABCD,∴FH⊥平面ABCD,
过H作HG⊥CD交直线CD于点G,连接FG,则FG⊥CD,
∴∠FGH即为二面角F-CD-E的平面角,tan∠FGH=
| 1 |
| 2 |
延长AB与DC交于点Q,设FH=a,则HG=2a,
又∵PA=AB=BC=
| 1 |
| 2 |
在Rt△HGQ中,HQ=4a,Rt△PHB中,BH=FH=a,则 BQ=3a,HA=2a,
∴λ=
| PF |
| PB |
| AH |
| AB |
| 2a |
| 3a |
| 2 |
| 3 |
(Ⅱ)解法二:以A为坐标原点如图建立空间直角坐标系,
设AB=1,则B(1,0,0) ,C(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
由λ=
| PF |
| PB |
| PF |
| PB |
 ,由已知得F(λ,0,1-λ)
,由已知得F(λ,0,1-λ)则
| CF |
| 1 |
| 2 |
| ||
| 2 |
| DF |
| 3 |
设平面FCD的法向量
| n |
由
|
| n |
| 3 |
| λ-2 |
| λ-1 |
又平面CDE的法向量为
| n |
由tanθ=
| 1 |
| 2 |
2
| ||
| 5 |
由cosθ=
| ||||
|
|
2
| ||
| 5 |
解得λ=
| 2 |
| 3 |
| 6 |
| 5 |
| 2 |
| 3 |
点评:本题考查直线与平面平行的证明,考查两线段比值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
若变量x,y满足约束条件
且z=3x+y的最小值为-8,则k=( )
|
| A、2 | B、-2 | C、3 | D、-3 |
已知函数f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值1,那么此函数在[-2,2]上的最小值是( )
| A、-39 | B、-31 |
| C、-7 | D、以上都不对 |
若实数x,y满足约束条件
,则2x+y的最大值是( )
|
A、
| ||
| B、3 | ||
| C、-2 | ||
| D、2 |
若双曲线
+
=1的离心率为
,则实数k的值为( )
| x2 |
| 3 |
| y2 |
| k |
| 3 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |