题目内容
如果一个球的外切圆锥的高是这个球的半径的3倍，则圆锥的侧面面积和球的表面积之比为 ．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：设出球的半径，利用三角形相似，求出圆锥的底面半径，然后求出球的表面积，圆锥的全面积，即可得到比值．
解答：
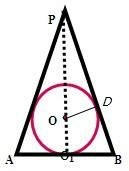解：设球的半径为1；圆锥的高为：3，则圆锥的底面半径为：r
由△POD∽△PO1B
=
=
，即
=
所以r=
圆锥的侧面积为：
×2
×2
π=6π，
球的表面积为：4π
所以圆锥的侧面积与球的表面积之比6π：4π=3：2．
故答案为：3：2．
解：设球的半径为1；圆锥的高为：3，则圆锥的底面半径为：r由△POD∽△PO1B
| OD |
| O1B |
| OP |
| PB |
| PD |
| PO1 |
| 1 |
| r |
| ||
| 3 |
所以r=
| 3 |
圆锥的侧面积为：
| 1 |
| 2 |
| 3 |
| 3 |
球的表面积为：4π
所以圆锥的侧面积与球的表面积之比6π：4π=3：2．
故答案为：3：2．
点评：本题考查圆锥的内接球，由题意画出图形，找出二者的关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=2x3-6x2+m（m为常数）在[-2，2]上有最大值1，那么此函数在[-2，2]上的最小值是（ ）
| A、-39 | B、-31 |
| C、-7 | D、以上都不对 |
若双曲线
+
=1的离心率为
，则实数k的值为（ ）
| x2 |
| 3 |
| y2 |
| k |
| 3 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |