题目内容
某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元.在满足需要的条件下,最少要花费 元.
考点:根据实际问题选择函数类型
专题:计算题,函数的性质及应用
分析:由题意设每袋35千克的购买x袋,每袋24千克的购买y袋;从而写出所有的情况并计算花费,从而求最小值即可.
解答:
解:设每袋35千克的购买x袋,每袋24千克的购买y袋;
∵需购某种化工原料106千克,
∴若x=0,y=5,此时共花费120×5=600元;
若x=1,y=3,此时共花费140+120×3=500元;
若x=2,y=2,此时共花费140×2+120×2=520元;
若x=3,y=1,此时共花费140×3+120=540元;
若x=4,y=0,此时共花费140×4=560元;
故最少要花费500元;
故答案为:500.
∵需购某种化工原料106千克,
∴若x=0,y=5,此时共花费120×5=600元;
若x=1,y=3,此时共花费140+120×3=500元;
若x=2,y=2,此时共花费140×2+120×2=520元;
若x=3,y=1,此时共花费140×3+120=540元;
若x=4,y=0,此时共花费140×4=560元;
故最少要花费500元;
故答案为:500.
点评:本题考查了学生将实际问题转化为数学问题的能力,属于中档题.

练习册系列答案
相关题目
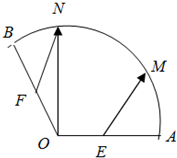 如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是
如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是
 阅读下边的程序,将输出的X的值依次分别记为x1,x2,x3,…,xn,…
阅读下边的程序,将输出的X的值依次分别记为x1,x2,x3,…,xn,…