题目内容
若向量
、
满足|
|=|
|=1，
•（
+
）=
，记
、
的夹角为θ，则函数y=sin（θx+
）的最小正周期为 ．
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| 3 |
| 2 |
| a |
| b |
| π |
| 6 |
考点：三角函数的周期性及其求法,数量积表示两个向量的夹角
专题：三角函数的图像与性质
分析：由条件根据两个向量的数量积的定义，求得cosθ=
，可得θ=
，函数y=sin（
x+
），再根据函数y=Asin（ωx+φ）的周期为
，得出结论．
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| ω |
解答：
解：由题意可得
2+
•
=1+cosθ=
，∴cosθ=
，∴θ=
．
故函数y=sin（
x+
）的最小正周期为
=6，
故答案为：6．
| a |
| a |
| b |
| 3 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
故函数y=sin（
| π |
| 3 |
| π |
| 6 |
| 2π | ||
|
故答案为：6．
点评：本题主要考查两个向量的数量积的定义，利用了函数y=Asin（ωx+φ）的周期为
，属于基础题．
| 2π |
| ω |
练习册系列答案
阅读快车系列答案
相关题目
若平面向量
=（1，x）和
=（2x+3，-x）互相平行，其中x∈R，则|
-
|=（ ）
| a |
| b |
| a |
| b |
| A、-2或0 | ||
| B、2.5 | ||
C、2或2
| ||
| D、2或10 |
过椭圆左焦点F且倾斜角为60°的直线与椭圆交于A、B两点，若
=
，则椭圆的离心率等于（ ）
| AF |
| 3 |
| 2 |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
+
在（0，1）上的最大值为（ ）
| x |
| 1-x |
A、
| ||
| B、1 | ||
| C、0 | ||
| D、不存在 |
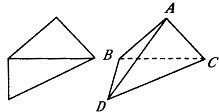如图是一副直角三角板．现将两三角板拼成直二面角，得到四面体ABCD，则下列叙述中正确的是．