题目内容
设x、y满足约束条件
，若目标函数z=ax+by（a＞0，b＞0）的最大值为6，则log3（
+
）的最小值为（ ）
|
| 1 |
| a |
| 2 |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用目标函数的几何意义，确定z取最大值点的最优解，利用基本不等式的性质，利用数形结合即可得到结论．
解答：
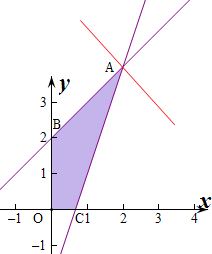解：作出不等式组对应的平面区域如图：
由z=ax+by（a＞0，b＞0）得y=-
x+
，
则直线的斜率k=-
＜0，截距最大时，z也最大．
平移直y=-
x+
，由图象可知当直线y=-
x+
经过点A时，
直线y=-
x+
的截距最大，此时z最大，
由
，解得
，
即A（2，4），
此时z=2a+4b=6，
即a+2b=3，
+
=1，
∴
+
=（
+
）（
+
）=
+
+
≥
+2
=
+
=3，
当且仅当
=
，即a=b=1时取等号，
此时log3（
+
）≥log33=1，
故选：A
解：作出不等式组对应的平面区域如图：由z=ax+by（a＞0，b＞0）得y=-
| a |
| b |
| z |
| b |
则直线的斜率k=-
| b |
| a |
平移直y=-
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
直线y=-
| a |
| b |
| z |
| b |
由
|
|
即A（2，4），
此时z=2a+4b=6，
即a+2b=3，
| a |
| 3 |
| 2b |
| 3 |
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| a |
| 3 |
| 2b |
| 3 |
| 5 |
| 3 |
| 2a |
| 3b |
| 2b |
| 3a |
| 5 |
| 3 |
|
| 5 |
| 3 |
| 4 |
| 3 |
当且仅当
| 2a |
| 3b |
| 2b |
| 3a |
此时log3（
| 1 |
| a |
| 2 |
| b |
故选：A
点评：本题主要考查线性规划的应用，利用z的几何意义先求出最优解是解决本题的关键，利用基本不等式的解法和结合数形结合是解决本题的突破点．
练习册系列答案
相关题目
在复平面内，复数z=
（i为虚数单位）的共轭复数对应的点位于（ ）
| 3-4i |
| 1+3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系，对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下：
由表中样本数据求得回归方程为
=bx+a，则点（a，b）与直线x+18y=100的位置关系是（ ）
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
 |
| y |
| A、点在直线左侧 |
| B、点在直线右侧 |
| C、点在直线上 |
| D、无法确定 |
已知函数f（x）=a x2-2bx+1（a＞0，a≠1）在区间（-∞，2]单调递减，且2a+b≤5，则
的取值范围为（ ）
| b+1 |
| a+2 |
A、（
| ||||
B、[
| ||||
C、[
| ||||
D、（
|
在平面直角坐标系xOy中，设D={（x，y）||x|≤2，|y|≤2}，E={（x，y）|x2+y2≤1}，向D中随机投一点，则所投点在E中的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
i是虚数单位，
=（ ）
| i |
| 1-i |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
下列命题中假命题是（ ）
| A、“存在x∈R，使得x2+x+1＜0”的否定是“对任意x∈R，均有x2+x+1≥0” | ||||||||
B、设随机变量ξ～N（0，1）．若P（ξ≥2）=p．则P（-2＜ξ＜0）=
| ||||||||
C、若函数y=lg（mx2-x-1）的值域为R，则m＜-
| ||||||||
D、若a＞0，b＞0，a+b=4．则
|