题目内容
已知
(x-1)+
(x-1)2+…+
(x-1)2014=a0+a1x+a2x2+…+a2014x2014,则a1+a2+…+a2013= .
| C | 1 2014 |
| C | 2 2014 |
| C | 2014 2014 |
考点:二项式系数的性质
专题:二项式定理
分析:在所给的等式中,令x=0,求得a0=0,再令x=1可得 0=a0+a1+a2+…+a2013,从而求得a1+a2+…+a2013 的值.
解答:
解:在
(x-1)+
(x-1)2+…+
(x-1)2014=a0+a1x+a2x2+…+a2014x2014 中,
令x=0,可得a0=0.
再令x=1可得 0=a0+a1+a2+…+a2013,∴a1+a2+…+a2013=0,
故答案为:0.
| C | 1 2014 |
| C | 2 2014 |
| C | 2014 2014 |
令x=0,可得a0=0.
再令x=1可得 0=a0+a1+a2+…+a2013,∴a1+a2+…+a2013=0,
故答案为:0.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.

练习册系列答案
相关题目
已知i是虚数单位,则复数z=i3•(-1+2i)的虚部为( )
| A、2i | B、i | C、2 | D、1 |
已知cos(π-α)=-
,则cos2α=( )
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|

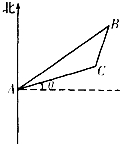 如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20
如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20