题目内容
已知函数f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,且2a+b≤5,则
的取值范围为( )
| b+1 |
| a+2 |
A、(
| ||||
B、[
| ||||
C、[
| ||||
D、(
|
考点:函数单调性的性质
专题:计算题,解三角形
分析:f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,可得a>1,b≥2,结合2a+b≤5,可得可行域,从而可求
的取值范围.
| b+1 |
| a+2 |
解答:
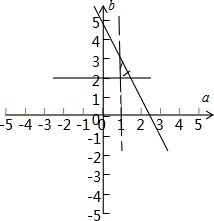 解:∵f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,
解:∵f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,
∴a>1,b≥2,
∵2a+b≤5,
∴可行域如图所示,交点坐标分别为(1,2),(1,3),(1.5,2),则
分别为1,
,
,
∴
的取值范围为[
,
).
故选:B.
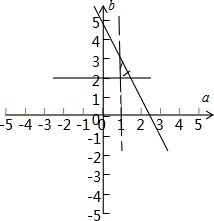 解:∵f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,
解:∵f(x)=a x2-2bx+1(a>0,a≠1)在区间(-∞,2]单调递减,∴a>1,b≥2,
∵2a+b≤5,
∴可行域如图所示,交点坐标分别为(1,2),(1,3),(1.5,2),则
| b+1 |
| a+2 |
| 4 |
| 3 |
| 6 |
| 7 |
∴
| b+1 |
| a+2 |
| 6 |
| 7 |
| 4 |
| 3 |
故选:B.
点评:本题考查函数的单调性,考查线性规划知识,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
一简单组合体的三视图及尺寸如图所示,则该组合体的体积是( )


| A、76 | B、80 | C、96 | D、112 |
若
=a+bi,(a,b∈R),则ab为( )
| 1 |
| 1-i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
执行如图所示的程序框图,输出的S值为( )


| A、9 | B、19 | C、20 | D、35 |
若关于x的不等式x2-3ax+2a2<0(a>0)的解集为(x1,x2),则x1+x2+
的取值范围是( )
| 2a |
| x1x2 |
A、(0,2
| ||
B、(0,2
| ||
C、[2
| ||
D、[2
|
已知集合A={x|0<x<6},B={x||x-2|<3},则A∩B=( )
| A、{x|-1<x<6} |
| B、{x|-1<x<5} |
| C、{x|0<x<3} |
| D、{x|0<x<5} |
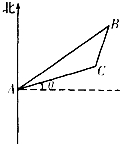 如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20
如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20