题目内容
已知函数f（x）=
，（a＞0，其中e为自然对数的底数），若关于x的方程f（f（x））=0，有且只有一个实数解，则实数a的取值范围为（ ）
|
| A、（1，+∞） |
| B、（1，2） |
| C、（0，1） |
| D、（0，1）∪（1，+∞） |
考点：函数的零点
专题：函数的性质及应用
分析：作出图象函数f（x）=
，（a＞0，其中e为自然对数的底数），得出f（1）=0，转化：关于x的方程f（f（x））=0，有且只有一个实数解，
f（x）=1，有且只有一个实数解，利用图象可判断分析．
|
f（x）=1，有且只有一个实数解，利用图象可判断分析．
解答：
解：∵函数f（x）=
，（a＞0，其中e为自然对数的底数），
∴图象如下：
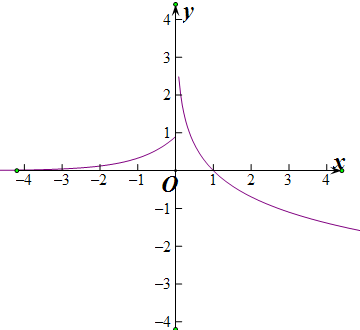
根据函数的图象可判断f（x）的零点为：1．
f（1）=0
∵关于x的方程f（f（x））=0，有且只有一个实数解，
∴f（x）=1，有且只有一个实数解，
∴根据图象可判断：0＜a＜1，
故选：C．
|
∴图象如下：
根据函数的图象可判断f（x）的零点为：1．
f（1）=0
∵关于x的方程f（f（x））=0，有且只有一个实数解，
∴f（x）=1，有且只有一个实数解，
∴根据图象可判断：0＜a＜1，
故选：C．
点评：本题考查了函数的图象和性质，运用数形结合的思想解决函数零点问题，属于中档题．
练习册系列答案
相关题目
不等式x2-3x+2＜0的解集是（ ）
| A、{x|x＜-2或x＞-1} |
| B、{x|x＜1或x＞2} |
| C、{x|1＜x＜2} |
| D、{x|-2＜x-1} |
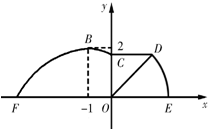如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC．该曲线段是函数y=Asin（ωx+
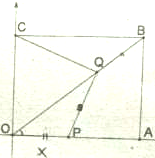如图，在矩形OABC中，O为原点，B点坐标为（8，6）．