��Ŀ����
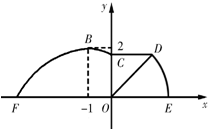 ��ͼ��ij�����ڵ�·EF��һ����һ���˶���������������ǰһ����Ϊ���߶�FBC�������߶��Ǻ���y=Asin����x+
��ͼ��ij�����ڵ�·EF��һ����һ���˶���������������ǰһ����Ϊ���߶�FBC�������߶��Ǻ���y=Asin����x+| 2�� |
| 3 |
| 3 |
��1����ص�ֵ�͡�DOE�Ĵ�С��
��2����Ҫ��Բ����������Ӧ������ODE�����ڽ�һ�������β�ƺ�������ε�һ���ڵ�·EF�ϣ�һ�������ڰ뾶OD�ϣ�����һ������P��Բ��DE�ϣ����β�ƺ����������ֵ�������ʱP���λ�ã�
���㣺���Ǻ��������Һ���,���������ʽ
ר�⣺���Ǻ�������ֵ,���Ǻ�����ͼ��������
��������1�����ȸ��ݺ�����ͼ����������Ľ���ʽ����һ����������
��2�����ã�1���Ľ��ۣ����������ʵ��Ӧ�ã�
��2�����ã�1���Ľ��ۣ����������ʵ��Ӧ�ã�
���
�⣺��1������������A=2��
=3��
��T=
��
����=
��
�����߶�FBC�Ľ���ʽΪ��y=2sin(
x+
)��
�൱x=0ʱ��y=OC=
��
��CD=
��
����COD=
������DOE=
��
��2���ɣ�1��֪OD=
��
�������β�ƺ����������ʱ��
��P �ڻ�DE�ϣ�
��OP=
��
���POE=�ȣ�0���ȡ�
��
�����β�ƺ�������Ϊ��
S=
sin��(
cos��-
sin��)=6(sin��cos��-sin2��)
=6(
sin2��+
cos2��-
)=3
sin(2��+
)-3��
��0���ȡ�
��
����2��+
=
ʱ��
��=
ʱ��
Sȡ�����ֵ3
-3��
| T |
| 4 |
��T=
| 2�� |
| �� |
����=
| �� |
| 6 |
�����߶�FBC�Ľ���ʽΪ��y=2sin(
| �� |
| 6 |
| 2�� |
| 3 |
�൱x=0ʱ��y=OC=
| 3 |
��CD=
| 3 |
����COD=
| �� |
| 4 |
| �� |
| 4 |
��2���ɣ�1��֪OD=
| 6 |
�������β�ƺ����������ʱ��
��P �ڻ�DE�ϣ�
��OP=
| 6 |
���POE=�ȣ�0���ȡ�
| �� |
| 4 |
�����β�ƺ�������Ϊ��
S=
| 6 |
| 6 |
| 6 |
=6(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| �� |
| 4 |
��0���ȡ�
| �� |
| 4 |
����2��+
| �� |
| 4 |
| �� |
| 2 |
��=
| �� |
| 8 |
Sȡ�����ֵ3
| 2 |
���������⿼���֪ʶҪ�㣺�����ͺ����Ľ���ʽ����������ʽ��ʵ��Ӧ�ã����ڻ������ͣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
��a=log0.20.3��b=log0.30.2��c=log0.30.1����a��b��c�Ĵ�С��ϵΪ��������
| A��a��b��c |
| B��b��a��c |
| C��c��a��b |
| D��c��b��a |
| a |
| b |
| a |
| b |
| A��2 | B��1 | C��0 | D��-2 |
��a��b��c�ֱ��Ǻ���f(x)=2x-log
x��g(x)=(
)x-log2x��h(x)=(
)x-log
x����㣬��a��b��c�Ĵ�С��ϵ�ǣ�������
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A��a��c��b |
| B��a��b��c |
| C��b��a��c |
| D��c��b��a |
��֪����f��x��=
����a��0������eΪ��Ȼ�����ĵ�������������x�ķ���f��f��x����=0������ֻ��һ��ʵ���⣬��ʵ��a��ȡֵ��ΧΪ��������
|
| A����1��+�ޣ� |
| B����1��2�� |
| C����0��1�� |
| D����0��1���ȣ�1��+�ޣ� |
 ��ͼ����֪E��F�ֱ��Ǿ���ABCD�ı�BC��CD���е㣬EF��AC���ڵ�G����
��ͼ����֪E��F�ֱ��Ǿ���ABCD�ı�BC��CD���е㣬EF��AC���ڵ�G����