题目内容
已知⊙O:x2+y2=4及点A(1,3),BC为⊙O的任意一条直径,则
•
= .
| AB |
| AC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:分类讨论:当直径BC所在的直线斜率存在时,设直线BC的方程为y=kx,与圆的方程联立得到根与系数的关系,再利用数量积运算即可得出;当直径BC所在的直线斜率不存在时,取B(0,-2),C(0,2),利用数量积即可得出.
解答:
解:如图所示,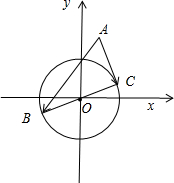
当直径BC所在的直线斜率存在时,设直线BC的方程为y=kx,
B(x1,y1),C(x2,y2),不妨是x1<x2.
则
•
=(x1-1,y1-3)•(x2-1,y2-3)
=(x1-1)(x2-1)+(kx1-3)(kx2-3)
=x1x2-(x1+x2)+1+k2x1x2-3k(x1+x2)+9
=(1+k2)x1x2-(1+3k)(x1+x2)+10,(*)
联立
,化为(1+k2)x2-4=0,
∴x1+x2=0,x1x2=-
.
代入(*)可得:
•
=
-0+10=6.
当直径BC所在的直线斜率不存在时,取B(0,-2),C(0,2).
则
•
=(-1,-5)•(-1,-1)=1+5=6.
综上可知:
•
=6.
故答案为:6.

当直径BC所在的直线斜率存在时,设直线BC的方程为y=kx,
B(x1,y1),C(x2,y2),不妨是x1<x2.
则
| AB |
| AC |
=(x1-1)(x2-1)+(kx1-3)(kx2-3)
=x1x2-(x1+x2)+1+k2x1x2-3k(x1+x2)+9
=(1+k2)x1x2-(1+3k)(x1+x2)+10,(*)
联立
|
∴x1+x2=0,x1x2=-
| 4 |
| 1+k2 |
代入(*)可得:
| AB |
| AC |
| -4(1+k2) |
| 1+k2 |
当直径BC所在的直线斜率不存在时,取B(0,-2),C(0,2).
则
| AB |
| AC |
综上可知:
| AB |
| AC |
故答案为:6.
点评:本题考查了数量积运算、直线与圆相交问题转化为方程联立得到根与系数的关系、分类讨论思想方法等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}为递增数列,则实数λ的取值范围为( )
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
在一次防恐演习中,某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击99次,则他最有可能射中目标( )次.
| A、99 | B、80 |
| C、79或80 | D、79 |
已知函数f(x)(x∈R)的图象上任一点(x0,y0)处切线的方程为:y-y0=(x0-2)( x0-1)(x-x0),那么函数f(x)的单调减区间是( )
| A、(1,2) |
| B、(-∞,1] |
| C、[2,+∞) |
| D、(-∞,-1) |
在复平面内,复数
-i3对应的点位于( )
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
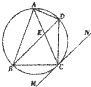 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=