题目内容

已知函数f（x）（x∈R）的图象上任一点（x0，y0）处切线的方程为：y-y0=（x0-2）（ x0-1）（x-x0），那么函数f（x）的单调减区间是（　　）
A、（1，2）
B、（-∞，1]
C、[2，+∞）
D、（-∞，-1）
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：计算题,导数的概念及应用
分析：由切线方程y-y0=（x0-2）（x0-1）（x-x0），可知任一点的导数为f′（x）=（x-2）（x-1），然后由f′（x）＜0，可求单调递减区间．
解答： 解：因为函数f（x），（x∈R）上任一点（x0y0）的切线方程为y-y0=（x0-2）（x0-1）（x-x0），
所以函数在任一点（x0y0）的切线斜率为k=（x0-2）（x0-1），
即知任一点的导数为f′（x）=（x-2）（x-1）．
由f′（x）=（x-2）（x-1）＜0，得1＜x＜2，
即函数f（x）的单调递减区间是（1，2）．
故选：A．
点评：本题的考点是利用导数研究曲线上某点切线方程，先由切线方程得到切线斜率，进而得到函数的导数，然后解导数不等式，是解决本题的关键．
练习册系列答案
相关题目
f（x）为R上的偶函数，且当x∈（-∞，0）时，f（x）=x（x-1），则当x∈（0，+∞）时，f（x）=
 
．
已知⊙O：x2+y2=4及点A（1，3），BC为⊙O的任意一条直径，则
AB
•
AC
=
 
．
已知函数f（x）=2x-2-x，则f（x）是（　　）
A、奇函数且是增函数
B、奇函数且是减函数
C、偶函数且是增函数
D、偶函数且是减函数
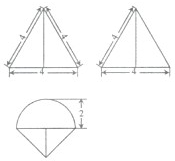
某简单组合体的三视图如图所示，则该组合体的体积为（　　）
A、
2
3
3
（π+2）
B、
4
3
3
（π+2）
C、
2
3
3
（π+
2
）
D、
8
3
3
（π+2）
已知sinα-sinβ=
6
3
，cosα-cosβ=
3
3
，则cos2
α-β
2
等于（　　）
A、
3
4
B、
1
2
C、
1
16
D、
1
4
已知集合A={x|x2＜4x}，集合B={y|y=-x2，-1≤x≤2}，则集合∁R（A∩B）=（　　）
A、RB、{0}
C、∅D、{x|x≥4或x≤0}
下列命题中，真命题的是（　　）
A、?0∈R，e x0≤0
B、?x∈R，2x＞x2
C、a-b＞0是a3-b3＞0的充分不必要条件
D、ab＞1是a＞1且b＞1的必要不充分条件
已知A={x|log2x＜2}，B={x|
1
3
＜3x＜
3
}，则A∩B为（　　）
A、（0，
1
2
）
B、（0，
2
）
C、（-1，
1
2
）
D、（-1，
2
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网