题目内容
若关于x的不等式（x-2）2＞ax2（a＞1）的解集中的整数恰有两个，则实数a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先将不等式变形为[
x+（x-2）][
x-（x-2）]＜0的形式，再求出解集由题意得到1＜
＜2，解出即可．
| a |
| a |
| 2 | ||
|
解答：
解：∵（x-2）2＞ax2，
∴ax2-（x-2）2＜0，
∵a＞1，
∴[
x+（x-2）][
x-（x-2）]＜0，
∴-
＜x＜
，
又
＜1，有两个整数解，
∴1＜
＜2，
解得：4＜a＜9，
故答案为：（4，9）．
∴ax2-（x-2）2＜0，
∵a＞1，
∴[
| a |
| a |
∴-
| 2 | ||
|
| 2 | ||
|
又
| 2 | ||
|
∴1＜
| 2 | ||
|
解得：4＜a＜9，
故答案为：（4，9）．
点评：考查学生解一元二次不等式的能力，运用一元二次不等式解决数学问题的能力．
练习册系列答案
53随堂测系列答案
相关题目
定义一种运算a?b=
，令f（x）=（3+2x-x2）?|x-t|（t为常数），且x∈[-3，3]，则使函数f（x）的最大值为3的t的集合是（ ）
|
| A、{3，-3} |
| B、{-1，5} |
| C、{3，-1} |
| D、{-3，-1，3，5} |
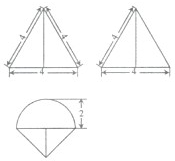
某简单组合体的三视图如图所示，则该组合体的体积为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知复数z=2+i，
是z的共轭复数，则
对应的点位于（ ）
. |
| z |
| ||
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |