题目内容
在一次防恐演习中，某射手击中目标的概率为0.8，每次射击的结果相互独立，现射击99次，则他最有可能射中目标（ ）次．
| A、99 | B、80 |
| C、79或80 | D、79 |
考点：相互独立事件的概率乘法公式
专题：概率与统计
分析：用射击次数乘以每次击中目标的概率，即得他击中目标次数的期望，从而求得他最有可能射中目标的次数．
解答：
解：由题意可得，他击中目标次数的期望为 99×0.8=79.2，
再根据击中目标次数为正整数，可得击中目标次数为79或80，
故选：C．
再根据击中目标次数为正整数，可得击中目标次数为79或80，
故选：C．
点评：本题考查相互独立事件的概率乘法公式，体现了转化的数学思想，属于中档题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
定义一种运算a?b=
，令f（x）=（3+2x-x2）?|x-t|（t为常数），且x∈[-3，3]，则使函数f（x）的最大值为3的t的集合是（ ）
|
| A、{3，-3} |
| B、{-1，5} |
| C、{3，-1} |
| D、{-3，-1，3，5} |
已知函数f（x）=2x-2-x，则f（x）是（ ）
| A、奇函数且是增函数 |
| B、奇函数且是减函数 |
| C、偶函数且是增函数 |
| D、偶函数且是减函数 |
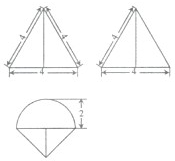
某简单组合体的三视图如图所示，则该组合体的体积为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知集合A={x|x2＜4x}，集合B={y|y=-x2，-1≤x≤2}，则集合∁R（A∩B）=（ ）
| A、R | B、{0} |
| C、∅ | D、{x|x≥4或x≤0} |
已知f（x）=
cos2x-sin2x，若y=f（x-m）（m＞0）是奇函数，则m的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|