题目内容
设奇函数f(x)满足f(x+2)=f(x-2),且当x∈[0,2]时,f(x)=x,则f(7tan
)= .
| 9π |
| 4 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,根据f(x+2)=f(x-2),得到f(x)的周期为4,然后,根据7tan
=7tan(2π+
)=7tan
=7,从而得到f(7tan
)=f(7)=f(2×4-1)=f(-1),最后,结合函数为奇函数进行求解.
| 9π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
解答:
解:∵f(x+2)=f(x-2),
∴f(x+4)=f(x),
∴f(x)的周期为4,
∵7tan
=7tan(2π+
)=7tan
=7,
∴f(7tan
)=f(7)=f(2×4-1)=f(-1)
∵f(x)是奇函数,
∴f(-1)=-f(1),
∵当x∈[0,2]时,f(x)=x,
∴f(1)=1,
∴f(-1)=-1,
∴f(7tan
)=-1,
故答案为:-1.
∴f(x+4)=f(x),
∴f(x)的周期为4,
∵7tan
| 9π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴f(7tan
| 9π |
| 4 |
∵f(x)是奇函数,
∴f(-1)=-f(1),
∵当x∈[0,2]时,f(x)=x,
∴f(1)=1,
∴f(-1)=-1,
∴f(7tan
| 9π |
| 4 |
故答案为:-1.
点评:本题重点考查了诱导公式、奇函数的性质、周期性等知识,属于综合性题目,属于中档题.

练习册系列答案
相关题目
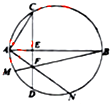 如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.
如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N.