题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{cosx,x<0}\end{array}\right.$,则f[f(-$\frac{π}{3}$)]=( )| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
分析 由已知得f(-$\frac{π}{3}$)=cos(-$\frac{π}{3}$)=cos$\frac{π}{3}$=$\frac{1}{2}$,从而f[f(-$\frac{π}{3}$)]=f($\frac{1}{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>0}\\{cosx,x<0}\end{array}\right.$,
∴f(-$\frac{π}{3}$)=cos(-$\frac{π}{3}$)=cos$\frac{π}{3}$=$\frac{1}{2}$,
f[f(-$\frac{π}{3}$)]=f($\frac{1}{2}$)=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
11.复数$\frac{(1+i)(3+4i)}{i}$等于( )
| A. | 7+i | B. | 7-i | C. | 7+7i | D. | -7+7i |
12.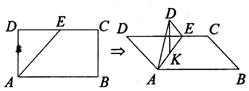 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
13.抛物线y2=2x的准线方程是( )
| A. | x=$\frac{1}{2}$ | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=-1 |
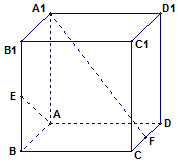 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.