题目内容
9.已知数列{an}满足a1=1,Sn=2an+1,其中Sn为{an}的前n项和(n∈N*).(Ⅰ)求S1,S2及数列{Sn}的通项公式;
(Ⅱ)若数列{bn}满足${b_n}=\frac{{{{(-1)}^n}}}{S_n}$,且{bn}的前n项和为Tn,求证:当n≥2时,$\frac{1}{3}≤|{T_n}|≤\frac{7}{9}$.
分析 (Ⅰ)根据数列的递推公式得到数列{Sn}为以1为首项,以$\frac{3}{2}$为公比的等比数列,即可求出通项公式,再代值计算即可,
(Ⅱ)先求出bn,再根据前n项和公式得到|Tn|,利用放缩法即可证明.
解答 解:(Ⅰ)数列{an}满足Sn=2an+1,则Sn=2an+1=2(Sn+1-Sn),即3Sn=2Sn+1,
∴$\frac{{{S_{n+1}}}}{S_n}=\frac{3}{2}$,
即数列{Sn}为以1为首项,以$\frac{3}{2}$为公比的等比数列,
∴Sn=($\frac{3}{2}$)n-1(n∈N*).
∴S1=1,S2=$\frac{3}{2}$;
(Ⅱ)在数列{bn}中,${b_n}=\frac{{{{(-1)}^n}}}{S_n}=-1×\frac{{{{(-1)}^{n-1}}}}{{{{(\frac{3}{2})}^{n-1}}}}$,
Tn为{bn}的前n项和,
则|Tn|=$|-1×\{1+(-\frac{2}{3})+\frac{4}{9}$$+[-{(\frac{2}{3})^3}]+…+\frac{{{{(-1)}^{n-1}}}}{{{{(&\frac{3}{2})}^{n-1}}}}\}|$|=$|1+(-\frac{2}{3})+\frac{4}{9}+$$[-{(\frac{2}{3})^3}]+…+\frac{{{{(-1)}^{n-1}}}}{{{{(\frac{3}{2})}^{n-1}}}}|$.
而当n≥2时,$1-\frac{2}{3}≤|1+(-\frac{2}{3})$$+\frac{4}{9}+[-{(\frac{2}{3})^3}]+…+$$\frac{{{{(-1)}^{n-1}}}}{{{{(\frac{3}{2})}^{n-1}}}}|≤|1+$$(-\frac{2}{3})+\frac{4}{9}|=\frac{7}{9}$,
即$\frac{1}{3}≤|{T_n}|≤\frac{7}{9}$.
点评 本题考查数列的通项及不等式的证明,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 2 |
| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
| A. | $\frac{1}{2(e-1)}$ | B. | $\frac{1}{4(e-1)}$ | C. | $\frac{1}{8(e-1)}$ | D. | $\frac{1}{16(e-1)}$ |
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的180名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
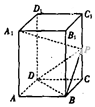 如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.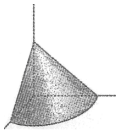 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).