题目内容
12.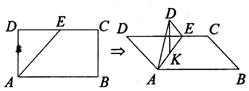 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
分析 根据图形的翻折过程中变与不变的量和位置关系知,若连接D'K,则∠D'KA=90°,得到K点的轨迹是以AD'为直径的圆上一弧,根据长方形的边长得到圆的半径,求得此弧所对的圆心角的弧度数,利用弧长公式求出轨迹长度.
解答  解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,
解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,
在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,
则∠D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,
根据长方形知圆半径是1,
如图当E与C重合时,AK=$\frac{2×2}{\sqrt{12+4}}$=1,
取O为AD′的中点,得到△OAK是正三角形.
故∠KOA=$\frac{π}{3}$,∴∠KOD'=$\frac{2π}{3}$,
其所对的弧长为$\frac{2π}{3}$,
故选:A.
点评 本题考查与二面角有关的立体几何综合题目,解题的关键是由题意得出点K的轨迹是圆上的一段弧,翻折问题中要注意位置关系与长度等数量的变与不变.本题是一个中档题目.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
2.在棱长为2的正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线D1E和BC1间的距离是( )
| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
3.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0,}&{\;}\\{x-y-1≤0,}&{\;}\\{x-1≥0.}&{\;}\end{array}\right.$若a∈[-2,9],则z=ax+y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值的概率为( )
| A. | $\frac{9}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
17.设数列{an}的前n项和为Sn,令Tn=$\frac{{S}_{1}+{S}_{2}+…+{S}_{n}}{n}$,称Tn为数列a1,a2,…,an的“平均和”,已知数列a1,a2,…,a670的“平均和”为2013,那么数列4,a1,a2,…,a670的“平均和”为( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
4.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点为F(-c,0)(c>0),过点F作圆${x^2}+{y^2}=\frac{a^2}{4}$的一条切线交圆于点E,交双曲线右支于点P,若$\overline{OP}=2\overline{OE}-\overline{OF}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 2 |
1.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{cosx,x<0}\end{array}\right.$,则f[f(-$\frac{π}{3}$)]=( )
| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
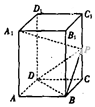 如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.