题目内容
6.已知集合U={1,2,3,4,5,6},A={1,2,3,5},B={3,5,6}.(Ⅰ)求A∩B;
(Ⅱ)求(∁UA)∪B.
分析 利用集合的基本运算即可得到结论.
解答 解:(Ⅰ)U={1,2,3,4,5,6},A={1,2,3,5},B={3,5,6}.
∴A∩B={3,5},
(Ⅱ)(∁UA)={4,6},
∴(∁UA)∪B={3,4,5,6}
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.设数列{an}的前n项和为Sn,令Tn=$\frac{{S}_{1}+{S}_{2}+…+{S}_{n}}{n}$,称Tn为数列a1,a2,…,an的“平均和”,已知数列a1,a2,…,a670的“平均和”为2013,那么数列4,a1,a2,…,a670的“平均和”为( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
1.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{cosx,x<0}\end{array}\right.$,则f[f(-$\frac{π}{3}$)]=( )
| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
11.下列语句为命题的是( )
| A. | lg100=2 | B. | 20172017是一个大数 | ||
| C. | 三角函数的图象真漂亮! | D. | 指数函数是递增函数吗? |
18.在区间[1,e]上任取实数a,在区间[0,2]上任取实数b,使函数f(x)=ax2+x+$\frac{1}{4}$b有两个相异零点的概率是( )
| A. | $\frac{1}{2(e-1)}$ | B. | $\frac{1}{4(e-1)}$ | C. | $\frac{1}{8(e-1)}$ | D. | $\frac{1}{16(e-1)}$ |
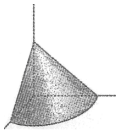 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,则堆放的米约有22斛(结果精确到个位).