抛物线y2=2x的准线方程是( )A．x=$\frac{1}{2}$B．x=1C．x=-$\frac{1}{2}$D．x=-1 题目和参考答案——青夏教育精英家教网——

题目内容

13．抛物线y²=2x的准线方程是（　　）

A．

x=$\frac{1}{2}$

B．

x=1

C．

x=-$\frac{1}{2}$

D．

x=-1

分析根据题意，由抛物线的标准方程分析可得其焦点位置以及p的值，进而由抛物线的准线方程计算可得答案．

解答解：根据题意，抛物线的标准方程为y²=2x，
则其焦点在x轴正半轴上，且p=1，
则其准线方程为x=-$\frac{1}{2}$，
故选：C．

点评本题考查抛物线的几何性质，关键是掌握抛物线标准方程的形式．

练习册系列答案

全程设计系列答案

小状元冲刺100分必选卷系列答案

新动力英语复合训练系列答案

初中语文阅读片段训练系列答案

北大绿卡名校中考模拟试卷汇编系列答案

初中学业水平考试模拟卷系列答案

河南中招复习与指导系列答案

金考卷初中毕业学业考试说明检测卷系列答案

数学中考模拟试题系列答案

金考卷著名重点中学领航中考冲刺试卷系列答案

相关题目

3．设x，y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0，}&{\;}\\{x-y-1≤0，}&{\;}\\{x-1≥0．}&{\;}\end{array}\right.$若a∈[-2，9]，则z=ax+y仅在点（$\frac{7}{3}$，$\frac{4}{3}$）处取得最大值的概率为（　　）

4．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左焦点为F（-c，0）（c＞0），过点F作圆${x^2}+{y^2}=\frac{a^2}{4}$的一条切线交圆于点E，交双曲线右支于点P，若$\overline{OP}=2\overline{OE}-\overline{OF}$，则双曲线的离心率为（　　）

$\frac{{\sqrt{10}}}{2}$

$\frac{{\sqrt{5}}}{2}$

$\frac{{\sqrt{7}}}{2}$

1．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x≥0}\\{cosx，x＜0}\end{array}\right.$，则f[f（-$\frac{π}{3}$）]=（　　）

cos$\frac{1}{2}$

-cos$\frac{1}{2}$

$\frac{\sqrt{2}}{2}$

±$\frac{\sqrt{2}}{2}$

8．已知π＜α＜$\frac{3π}{2}$，sinα=-$\frac{4}{5}$．
（Ⅰ）求cosα的值；
（Ⅱ）求sin2α+3tanα的值．

18．在区间[1，e]上任取实数a，在区间[0，2]上任取实数b，使函数f（x）=ax²+x+$\frac{1}{4}$b有两个相异零点的概率是（　　）

$\frac{1}{2（e-1）}$

$\frac{1}{4（e-1）}$

$\frac{1}{8（e-1）}$

$\frac{1}{16（e-1）}$

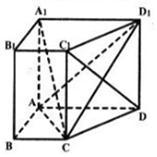如图，在直四棱柱ABCD-A₁B₁C₁D₁中，底面四边形ABCD是直角梯形，其中
AB⊥AD，AB=BC=1，AD=2，AA₁=$\sqrt{2}$．
（Ⅰ）求证：直线C₁D⊥平面ACD₁；
（Ⅱ）试求三棱锥A₁-ACD₁的体积．

2．已知指数函数f（x）=a^x（a＞0且a≠1）的图象过点P（2，4），则在（0，10]内任取一个实数x，使得f（x）＞16的概率为$\frac{3}{5}$．

3．若直线mx+2y+m=0与直线3mx+（m-1）y+7=0平行，则m的值为（　　）