题目内容
16.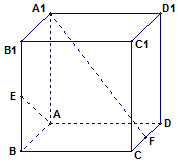 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.(Ⅰ)求AE与A1F所成角的大小;
(Ⅱ)求AE与平面ABCD所成角的正切值.
分析 (Ⅰ)建立坐标系,利用向量方法求AE与A1F所成角的大小;
(Ⅱ)证明∠EAB就是AE与平面ABCD所成角,即可求AE与平面ABCD所成角的正切值.
解答 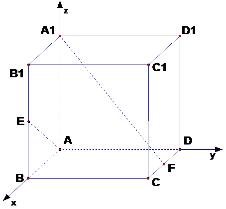 解:(Ⅰ)如图,建立坐标系A-xyz,则A(0,0,0),E(1,0,$\frac{1}{2}$),A1(0,0,1),F($\frac{1}{2}$,1,0)
解:(Ⅰ)如图,建立坐标系A-xyz,则A(0,0,0),E(1,0,$\frac{1}{2}$),A1(0,0,1),F($\frac{1}{2}$,1,0)
$\overrightarrow{AE}$=(1,0,$\frac{1}{2}$),$\overrightarrow{{A}_{1}F}$=($\frac{1}{2}$,1,-1)
∴$\overrightarrow{AE}•\overrightarrow{{A}_{1}F}$=0,
所以AE与A1F所成角为90°-------------------------------------(6分)
(Ⅱ)∵ABCD-A1B1C1D1是正方体,
∴BB1⊥平面ABCD
∴∠EAB就是AE与平面ABCD所成角,又E是BB1中点,
在直角三角形EBA中,tan∠EAB=$\frac{1}{2}$.-----------------------(13分)
点评 本题考查异面直线所成角,线面角,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
4.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点为F(-c,0)(c>0),过点F作圆${x^2}+{y^2}=\frac{a^2}{4}$的一条切线交圆于点E,交双曲线右支于点P,若$\overline{OP}=2\overline{OE}-\overline{OF}$,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 2 |
11.在空间,可以确定一个平面的条件是( )
| A. | 两条直线 | B. | 一点和一条直线 | C. | 三个点 | D. | 一个三角形 |
1.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{cosx,x<0}\end{array}\right.$,则f[f(-$\frac{π}{3}$)]=( )
| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
6.用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 是正确的 |
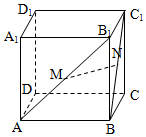 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.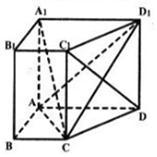 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中