题目内容
11.复数$\frac{(1+i)(3+4i)}{i}$等于( )| A. | 7+i | B. | 7-i | C. | 7+7i | D. | -7+7i |
分析 根据复数的运算法则计算即可.
解答 解:$\frac{(1+i)(3+4i)}{i}$=$\frac{-1+7i}{i}$=$\frac{(-1+7i)i}{{i}^{2}}$=7+i,
故选:A.
点评 本题考查复数的运算,涉及复数的化简,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.同时具有性质:①图象的相邻两条对称轴间的距离是$\frac{π}{2}$;②在[-$\frac{π}{6}$,$\frac{π}{3}$]上是增函数的一个函数为( )
| A. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos($\frac{x}{2}$-$\frac{π}{6}$) |
2.在棱长为2的正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线D1E和BC1间的距离是( )
| A. | $\frac{2\sqrt{6}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
3.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0,}&{\;}\\{x-y-1≤0,}&{\;}\\{x-1≥0.}&{\;}\end{array}\right.$若a∈[-2,9],则z=ax+y仅在点($\frac{7}{3}$,$\frac{4}{3}$)处取得最大值的概率为( )
| A. | $\frac{9}{11}$ | B. | $\frac{7}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
1.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{cosx,x<0}\end{array}\right.$,则f[f(-$\frac{π}{3}$)]=( )
| A. | cos$\frac{1}{2}$ | B. | -cos$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | ±$\frac{\sqrt{2}}{2}$ |
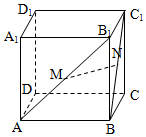 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AB1、BC1的中点.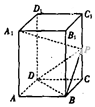 如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.
如图,已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,高AA1=4$\sqrt{2}$,P为CC1的中点.