题目内容
菱形ABCD所在平面外有一点P，且PC⊥平面ABCD，则PA于对角线BD的位置关系是异面且垂直 （判断对错）
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由已知得AC⊥BD，PC⊥BD，从而BD⊥平面PAC，由此能证明PA于对角线BD的位置关系是异面且垂直．
解答：
解：∵菱形ABCD所在平面外有一点P，且PC⊥平面ABCD，
∴AC⊥BD，PC⊥BD，
∴BD⊥平面PAC，
∵PA?平面PAC，
∴BD⊥PA，
∴PA于对角线BD的位置关系是异面且垂直．
故答案为：正确．
解：∵菱形ABCD所在平面外有一点P，且PC⊥平面ABCD，∴AC⊥BD，PC⊥BD，
∴BD⊥平面PAC，
∵PA?平面PAC，
∴BD⊥PA，
∴PA于对角线BD的位置关系是异面且垂直．
故答案为：正确．
点评：本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
名校课堂系列答案
相关题目
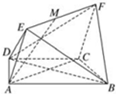如图，在多面体ABCDEF中，四边形ABCD是梯形，AB∥CD，四边形ACFE是矩形，平面ACFE⊥平面ABCD，AD=DC=CB=a，∠ACB=