Question

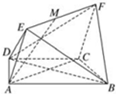如图，在多面体ABCDEF中，四边形ABCD是梯形，AB∥CD，四边形ACFE是矩形，平面ACFE⊥平面ABCD，AD=DC=CB=a，∠ACB=

π

2

．
（1）求证：BC⊥平面ACFE；
（2）若M是棱EF上一点，AM∥平面BDF，求EM的长．

Answer 1

考点：直线与平面平行的判定,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）根据线面垂直的判定定理，即可证明：BC⊥平面ACFE；
（2）根据线面平行的判定定理，确定EM的长度，然后根据AM∥平面BDF的判定定理即可得到结论．

解答： （1）证明：在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ACB=

π

2

．
∴AC⊥BC
又∵平面ACFE⊥平面ABCD，交线为AC，
∴BC⊥平面ACFE
（2）解：当EM=

3

3

a时，AM∥平面BDF；
在梯形ABCD中，设AC∩BD=N，连接FN，则CN：NA=1：2，AD=DC=CB=a，AB∥CD，
所以∠ACD=∠CAB=∠DAC，
所以∠ABC+∠BCD=∠DAB+∠ACD+∠ACB=3∠DAC+

π

2

=π，
所以∠DAC=

π

6

，即∠CBN=

π

6

．
又∠ACB=

π

2

，CB=a，
所以CN=

3

3

a，
连接FN，由AM∥平面BDF得AM∥FN，
因为四边形ACFE是矩形，所以EM=CN=

3

3

a．

点评：本题考查了空间几何体中线面关系的判断及证明；关键是熟练判定定理及性质定理．