题目内容
若3cosβ+4sinβ=5，则tanβ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
| D、1 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用同角三角函数间的基本关系得到sin2β+cos2β=1，与已知等式联立即可求出sinβ与cosβ的值，即可确定出tanβ的值．
解答：
解：联立得：
，
解得：sinβ=
，cosβ=
，
则tanβ=
=
．
故选：B．
|
解得：sinβ=
| 4 |
| 5 |
| 3 |
| 5 |
则tanβ=
| sinβ |
| cosβ |
| 4 |
| 3 |
故选：B．
点评：此题考查了同角三角基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
在△ABC中，“A＜B”是“sin2A＜sin2B”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
假设a1，a2，a3，a4是一个等差数列，且满足0＜a1＜2，a3=4．若bn=2an（n=1，2，3，4）．给出以下命题：
①数列{bn}是等比数列；
②b2＞4；
③b4＞32；
④b2b4=256．
其中正确命题的个数是（ ）
①数列{bn}是等比数列；
②b2＞4；
③b4＞32；
④b2b4=256．
其中正确命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
曲线C1：y=
ex关于直线y=x对称得曲线C2，动点P在C1上，动点Q在C2上，则|PQ|最小值为（ ）
| 1 |
| 2 |
| A、1-ln2 | ||
B、
| ||
| C、1+ln2 | ||
D、
|
下列求导运算正确的是（ ）
①（x+
）′=1+
②（log2x）′=
③（3x）′=3xlog3e
④（x2cosx）′=-2xsinx
⑤（
）′=
⑥（exln（2x-5））′=exln（2x-5）+
．
①（x+
| 1 |
| x |
| 1 |
| x2 |
②（log2x）′=
| 1 |
| xln2 |
③（3x）′=3xlog3e
④（x2cosx）′=-2xsinx
⑤（
| ex+1 |
| ex-1 |
| -2ex |
| (ex-1)2 |
⑥（exln（2x-5））′=exln（2x-5）+
| ex |
| 2x-5 |
| A、①②③ | B、②④⑤ |
| C、②⑤ | D、②⑤⑥ |
已知长方形ABCD，抛物线l以CD的中点E为顶点，经过A、B两点，记拋物线l与AB边围成的封闭区域为M．若随机向该长方形内投入一粒豆子，落入区域M的概率为P．则下列结论正确的是（ ）
| A、不论边长AB，BC如何变化，P为定值 | ||
B、若
| ||
| C、当且仅当AB=BC时，P最大 | ||
| D、当且仅当AB=BC时，P最小 |
在△ABC中，已知a=1，b=
，A=30°，B为锐角，那么角A，B，C的大小关系为（ ）
| 3 |
| A、A．＞B＞C |
| B、B＞A＞C |
| C、C＞B＞A |
| D、C＞A＞B |
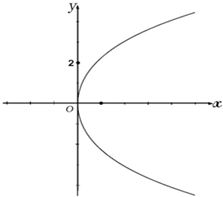已知曲线Γ：y2=4x，直线l经过点（0，2）且其一个方向向量为