题目内容
在△ABC中，已知a=1，b=
，A=30°，B为锐角，那么角A，B，C的大小关系为（ ）
| 3 |
| A、A．＞B＞C |
| B、B＞A＞C |
| C、C＞B＞A |
| D、C＞A＞B |
考点：正弦定理
专题：解三角形
分析：利用正弦定理，求得sinB的值，进而求得B，进而利用三角形内角和求得C，最后判断三个角的大小．
解答：
解：∵
=
，
∴sinB=
•sinA=
×
=
，
∴B=
或
∵B为锐角
∴B=
，
∴C=π-
-
=
，
∴C＞B＞A，
故选：C．
| a |
| sinA |
| b |
| sinB |
∴sinB=
| b |
| a |
| ||
| 1 |
| 1 |
| 2 |
| ||
| 2 |
∴B=
| π |
| 3 |
| 2π |
| 3 |
∵B为锐角
∴B=
| π |
| 3 |
∴C=π-
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴C＞B＞A，
故选：C．
点评：本题主要考查了正弦定理的应用．考查了学生的基础知识的熟练掌握．
练习册系列答案
相关题目
抛物线y2=8x上到其焦点F距离为5的点有（ ）
| A、0个 | B、1个 | C、2个 | D、4个 |
已知向量
=（2，-3，5）与向量
=（3，λ，
）平行，则λ=（ ）
| a |
| b |
| 15 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若3cosβ+4sinβ=5，则tanβ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
| D、1 |
已知△ABC中，AB=
，BC=1，sinC=
cosC，则△ABC的面积为（ ）
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知曲线y=g（x）在点（1，g（1））处的切线方程为y=2x+1，设函数f（x）=g（2x-1），则曲线y=f（x）在点（1，f（1））处切线方程为（ ）
| A、y=2x+1 |
| B、y=4x-1 |
| C、y=2x-1 |
| D、y=4x+1 |
若P是抛物线x2=4y上的一个动点，则点P到直线l1：y=-1，l2：3x+4y+12=0的距离之和的最小值为（ ）
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
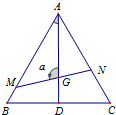如图，△ABC是边长为1的正三角形，M，N分别是边AB，AC上的点，线段MN过△ABC的重心G，设∠MGA=α，α∈[