题目内容
已知圆C:x2+y2-2y-4=0,直线l:y=mx+1-m;
(1)求证:对任意m∈R,直线l与圆C总有两个不同的交点;
(2)求l与圆C交于A,B两点,若|AB|=
,求l的倾斜角.
(1)求证:对任意m∈R,直线l与圆C总有两个不同的交点;
(2)求l与圆C交于A,B两点,若|AB|=
| 17 |
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)由直线系方程求得直线过定点,再由定点在圆内得结论;
(2)由弦长及圆的半径求得弦心距,再由圆心到直线的距离列式求得m的值,则直线l的倾斜角可求.
(2)由弦长及圆的半径求得弦心距,再由圆心到直线的距离列式求得m的值,则直线l的倾斜角可求.
解答:
(1)证明:圆C:x2+y2-2y-4=0可化为:x2+(y-1)2=5.
由直线l:y=mx+1-m,得m(x-1)-y+1=0,
由
,得
.
∴直线l:mx-y+1-m=0过定点P(1,1),
代入圆C:x2+(y-1)2=5,得12+(1-1)2=1<5,
∴点P(1,1)在圆C:x2+(y-1)2=5内部,
∴对任意的m,直线l与圆C总有两个不同的交点;
(2)解:当直线l的斜率不存在时,直线方程为x=1,代入圆x2+(y-1)2=5得:y1=-1,y2=3,
此时|AB|=4,不满足题意;
∴直线l的斜率存在,
由|AB|=
,圆的半径为
,得圆心到直线l:mx-y+1-m=0的距离为
=
.
则
=
,解得:m=±
.
∴直线l的倾斜角为60°或120°.
由直线l:y=mx+1-m,得m(x-1)-y+1=0,
由
|
|
∴直线l:mx-y+1-m=0过定点P(1,1),
代入圆C:x2+(y-1)2=5,得12+(1-1)2=1<5,
∴点P(1,1)在圆C:x2+(y-1)2=5内部,
∴对任意的m,直线l与圆C总有两个不同的交点;
(2)解:当直线l的斜率不存在时,直线方程为x=1,代入圆x2+(y-1)2=5得:y1=-1,y2=3,
此时|AB|=4,不满足题意;
∴直线l的斜率存在,
由|AB|=
| 17 |
| 5 |
5-
|
| ||
| 2 |
则
| |-m| | ||
|
| ||
| 2 |
| 3 |
∴直线l的倾斜角为60°或120°.
点评:本题考查了直线与圆的方程的应用,考查了直线系方程,考查了直线与圆的位置关系,训练了点到直线的距离公式的用法,体现了数学转化思想方法,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
若3cosβ+4sinβ=5,则tanβ=( )
A、-
| ||
B、
| ||
C、-
| ||
| D、1 |
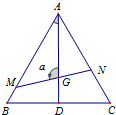 如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[
如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[