题目内容
 已知曲线Γ:y2=4x,直线l经过点(0,2)且其一个方向向量为
已知曲线Γ:y2=4x,直线l经过点(0,2)且其一个方向向量为| d |
(1)若曲线Γ的焦点F在直线l上,求实数k的值;
(2)当k=-1时,直线l与曲线Γ相交于A、B两点,求|AB|的值;
(3)当k(k>0)变化且直线l与曲线Γ有公共点时,是否存在这样的实数a,使得点P(a,0)关于直线l的对称点Q(x0,y0)落在曲线Γ的准线上.若存在,求出a的值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)确定F(1,0),k=
=-2,可得结论;
(2)确定直线l:y=-x+2l与曲线Γ的方程联立消去y并整理,利用弦长公式求|AB|的值;
(3)假设存在这样的实数a,使得点P(a,0)关于直线l的对称点Q(x0,y0)落在曲线Γ的准线上,直线l与曲线Γ的方程联立消去y并整理,求出Q的横坐标,求出a的值.
| 0-2 |
| 1-0 |
(2)确定直线l:y=-x+2l与曲线Γ的方程联立消去y并整理,利用弦长公式求|AB|的值;
(3)假设存在这样的实数a,使得点P(a,0)关于直线l的对称点Q(x0,y0)落在曲线Γ的准线上,直线l与曲线Γ的方程联立消去y并整理,求出Q的横坐标,求出a的值.
解答:
 解:(1)由y2=4x得,p=2,所以F(1,0),k=
解:(1)由y2=4x得,p=2,所以F(1,0),k=
=-2,
所以k=-2…(3分)
(2)当k=-1时,
=(1,k)=(1,-1),直线l:y=-x+2…(4分)
将直线l与曲线Γ的方程联立消去y并整理得,x2-8x+4=0,其中△>0…(6分)
设A(x1,y1)、B(x2,y2),则x1+x2=8,x1x2=4…(7分)
于是|AB|=
|x1-x2|=4
…(9分)
(3)假设存在这样的实数a,使得点P(a,0)关于直线l的对称点Q(x0,y0)落在曲线Γ的准线上,
根据题意可得k>0,所以直线l:y=kx+2,由于k>0,
直线l与曲线Γ的方程联立消去y并整理得,k2x2+4(k-1)x+4=0,
直线l与曲线Γ有公共点,故△=16(k-1)2-16k2≥0,解得k≤
,所以0<k≤
…(11分)
点P(a,0)关于直线l的对称点Q(x0,y0),则
…(12分)
得x0=
(0<k≤
)…(13分),
当点Q落在曲线Γ的准线x=-1上时,
=-1,
所以a=1-
,即
=-
…(14分)
当k=
时,a=1;当0<k<
时,
=(k-
)-
+1>2,解得-1<a<1
所以-1≤a≤1,所以存在这样的实数a,满足题设条件.…(16分)
 解:(1)由y2=4x得,p=2,所以F(1,0),k=
解:(1)由y2=4x得,p=2,所以F(1,0),k=| 0-2 |
| 1-0 |
所以k=-2…(3分)
(2)当k=-1时,
| d |
将直线l与曲线Γ的方程联立消去y并整理得,x2-8x+4=0,其中△>0…(6分)
设A(x1,y1)、B(x2,y2),则x1+x2=8,x1x2=4…(7分)
于是|AB|=
| 1+k2 |
| 6 |
(3)假设存在这样的实数a,使得点P(a,0)关于直线l的对称点Q(x0,y0)落在曲线Γ的准线上,
根据题意可得k>0,所以直线l:y=kx+2,由于k>0,
直线l与曲线Γ的方程联立消去y并整理得,k2x2+4(k-1)x+4=0,
直线l与曲线Γ有公共点,故△=16(k-1)2-16k2≥0,解得k≤
| 1 |
| 2 |
| 1 |
| 2 |
点P(a,0)关于直线l的对称点Q(x0,y0),则
|
得x0=
| a(1-k2)-4k |
| 1+k2 |
| 1 |
| 2 |
当点Q落在曲线Γ的准线x=-1上时,
| a(1-k2)-4k |
| 1+k2 |
所以a=1-
4(k-
| ||
| k2-1 |
| a-1 |
| 4 |
k-
| ||
| k2-1 |
当k=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 1-a |
| 1 |
| 2 |
| ||
k-
|
所以-1≤a≤1,所以存在这样的实数a,满足题设条件.…(16分)
点评:本题考查直线与圆锥曲线的综合问题,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“φ=
”是“cosφ=0”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若3cosβ+4sinβ=5,则tanβ=( )
A、-
| ||
B、
| ||
C、-
| ||
| D、1 |
已知曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,设函数f(x)=g(2x-1),则曲线y=f(x)在点(1,f(1))处切线方程为( )
| A、y=2x+1 |
| B、y=4x-1 |
| C、y=2x-1 |
| D、y=4x+1 |
若P是抛物线x2=4y上的一个动点,则点P到直线l1:y=-1,l2:3x+4y+12=0的距离之和的最小值为( )
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
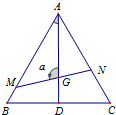 如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[
如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[