题目内容
假设a1,a2,a3,a4是一个等差数列,且满足0<a1<2,a3=4.若bn=2an(n=1,2,3,4).给出以下命题:
①数列{bn}是等比数列;
②b2>4;
③b4>32;
④b2b4=256.
其中正确命题的个数是( )
①数列{bn}是等比数列;
②b2>4;
③b4>32;
④b2b4=256.
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用,等差数列的通项公式,等比数列的通项公式
专题:等差数列与等比数列
分析:①中,由a1,a2,a3,a4是等差数列,判定bn=2an组成等比数列;
②中,由等差中项求出a2=
>2,得b2>4;
③中,由a4=a3+d>5,得出b4>25;
④中,求出b2b4=b32=256.
②中,由等差中项求出a2=
| a1+a3 |
| 2 |
③中,由a4=a3+d>5,得出b4>25;
④中,求出b2b4=b32=256.
解答:
解:根据题意,得
对于①,∵a1,a2,a3,a4是一个等差数列,
设公差为d,则an=a1+(n-1)d,(n=1,2,3,4);
∴bn=2an=2a1+(n-1)d=2a1•(2d)n-1,(n=1,2,3,4),
∴{bn}是首项为2a1,公比为2d的等比数列.∴命题①正确.
对于②,∵在等差数列{an}中,0<a1<2,a3=4,
∴a2=
=
>2,∴b2=2a2>4;
∴②正确.
对于③,等差数列{an}中,0<a1<2,a3=4,∴公差d∈(1,2),
∴a4=a3+d>5,∴b4=2a4>25=32;
∴命题③正确.
对于④,∵b2b4=b32=(2a3)2=(24)2=256,∴命题④正确.
综上,以上命题正确的是4个.
故选:D.
对于①,∵a1,a2,a3,a4是一个等差数列,
设公差为d,则an=a1+(n-1)d,(n=1,2,3,4);
∴bn=2an=2a1+(n-1)d=2a1•(2d)n-1,(n=1,2,3,4),
∴{bn}是首项为2a1,公比为2d的等比数列.∴命题①正确.
对于②,∵在等差数列{an}中,0<a1<2,a3=4,
∴a2=
| a1+a3 |
| 2 |
| a1+4 |
| 2 |
∴②正确.
对于③,等差数列{an}中,0<a1<2,a3=4,∴公差d∈(1,2),
∴a4=a3+d>5,∴b4=2a4>25=32;
∴命题③正确.
对于④,∵b2b4=b32=(2a3)2=(24)2=256,∴命题④正确.
综上,以上命题正确的是4个.
故选:D.
点评:本题考查了等差与等比数列的综合应用问题,解题时应熟练地应用等差、等比数列的性质,是一道综合题.

练习册系列答案
相关题目
抛物线y2=8x上到其焦点F距离为5的点有( )
| A、0个 | B、1个 | C、2个 | D、4个 |
“φ=
”是“cosφ=0”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知复数z满足z•(1-i)=3+i,i为虚数单位,则|z|=( )
A、
| ||
B、
| ||
| C、5 | ||
| D、3 |
已知向量
=(2,-3,5)与向量
=(3,λ,
)平行,则λ=( )
| a |
| b |
| 15 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若3cosβ+4sinβ=5,则tanβ=( )
A、-
| ||
B、
| ||
C、-
| ||
| D、1 |
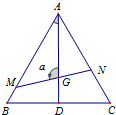 如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[
如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[