Question

曲线C₁：y=

1

2

e^x关于直线y=x对称得曲线C₂，动点P在C₁上，动点Q在C₂上，则|PQ|最小值为（　　）

• A、1-ln2
• B、

  2

  （1-ln2）
• C、1+ln2
• D、

  2

  （1+ln2）

Answer 1

考点：利用导数研究曲线上某点切线方程

专题：导数的综合应用

分析：根据函数关于y=x，求出函数的反函数，利用曲线关于y=x对称的性质，只要求出P到直线y=x的距离的最小值即可得到结论．

解答： 解：y=

1

2

e^x关于直线y=x对称得曲线C₂，
∴由y=

1

2

e^x，得e^x=2y，
即x=ln2y，
∴函数y=

1

2

e^x的反函数为y=ln2x，即曲线C₂：y=ln2x，
则要使|PQ|取得最小值，
则只需y=

1

2

e^x，上的点到直线y=x的距离最小即可，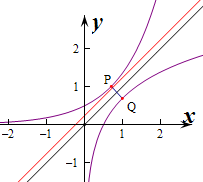
y′=f′（x）=

1

2

e^x，
由y′=f′（x）=

1

2

e^x=1，
得e^x=2，解得x=ln2，即切点P的横坐标为ln2，此时y=y=

1

2

e^ln2=1，
即P（ln2，1），则P到直线y=x的距离d=

|ln2-1|

2

=

(1-ln2) 2

2

，
∴|PQ|最小值=2d=

2

（1-ln2），
故选：B．

点评：本题主要考查两点间距离的求法，利用函数y=x的对称性，利用导数求出最小值是解决本题的关键，综合性较强．