题目内容
已知关于x的方程|5x-4|+a=0无解,|4x-3|+b=0有两个解,|3x-2|+c=0只有一个解,则化简|a-c|+|c-b|-|a-b|的结果是 .
考点:进行简单的演绎推理
专题:函数的性质及应用
分析:由于关于x的方程|5x-4|+a=0无解,可得a>0.方程|4x-3|+b=0变为|4x-3|=-b,根据|4x-3|+b=0有两个解,可得-b>0.方程|3x-2|+c=0变为|3x-2|=-c,由于只有一个解,可得-c=0.
解答:
解:由于关于x的方程|5x-4|+a=0无解,则a>0.
方程|4x-3|+b=0变为|4x-3|=-b,∵|4x-3|+b=0有两个解,∴-b>0,解得b<0.
方程|3x-2|+c=0变为|3x-2|=-c,由于只有一个解,∴-c=0,解得c=0.
∴|a-c|+|c-b|-|a-b|=a-b-(a-b)=0.
故答案为:0.
方程|4x-3|+b=0变为|4x-3|=-b,∵|4x-3|+b=0有两个解,∴-b>0,解得b<0.
方程|3x-2|+c=0变为|3x-2|=-c,由于只有一个解,∴-c=0,解得c=0.
∴|a-c|+|c-b|-|a-b|=a-b-(a-b)=0.
故答案为:0.
点评:本题考查了绝对值的意义、方程的解,考查了推理能力,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
若a≠0,b≠,则代数式
+
+
的取值共有( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、2个 | B、3个 | C、4个 | D、5个 |
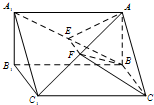 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.