题目内容
数列{an}中，a1，a2，a3成等差数列，a2，a3，a4成等比数列，a3，a4，a5的倒数成等差数列，则a1，a3，a5成 数列．
考点：等比数列的性质,等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差中项、等比中项的定义，即可得出结论．
解答：
解：∵a1，a2，a3成等差数列，
∴2a2=a1+a3，
∵a2，a3，a4成等比数列，
∴a32=a2a4，
∴2a32=（a1+a3）a4，
又a3，a4，a5的倒数成等差数列，
∴
=
+
，
∴
=
+
，
∴a32=a1a5，
∴a1，a3，a5成等比数列．
故答案为：等比．
∴2a2=a1+a3，
∵a2，a3，a4成等比数列，
∴a32=a2a4，
∴2a32=（a1+a3）a4，
又a3，a4，a5的倒数成等差数列，
∴
| 2 |
| a4 |
| 1 |
| a3 |
| 1 |
| a5 |
∴
| a1+a3 |
| a32 |
| 1 |
| a3 |
| 1 |
| a5 |
∴a32=a1a5，
∴a1，a3，a5成等比数列．
故答案为：等比．
点评：本题考查等差中项、等比中项的定义，考查学生的计算能力，正确运用等差中项、等比中项的定义是关键．
练习册系列答案
相关题目
《张丘建算经》卷上第22题--“女子织布”问题：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线y=2x+b被圆（x+1）2+y2=4所截得的弦最长，则b等于（ ）
| A、-1 | B、0 | C、1 | D、2 |
已知数列{an}中，a1=25，4an+1=4an-7（n∈N*），若其前n项和为Sn，则Sn的最大值为（ ）
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|
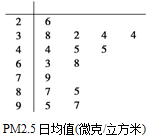通常把大气中直径小于或等于2.5微米的颗粒物（也称为可入肺颗粒物）称为PM2.5．我国PM2.5标准采用世卫组织设定的最宽限值，空气质量与PM2.5的关系如下表：