题目内容
已知数列{an}中,a1=25,4an+1=4an-7(n∈N*),若其前n项和为Sn,则Sn的最大值为( )
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|
考点:等差关系的确定,数列递推式
专题:点列、递归数列与数学归纳法
分析:由已知递推式得到数列{an}为等差数列,写出等差数列的前n项和公式,由二次函数最值的求法结合
n∈N*求Sn的最大值.
n∈N*求Sn的最大值.
解答:
解:由4an+1=4an-7,得:
an+1=an-
,即an+1-an=-
.
∴数列{an}是以a1=25为首项,以-
为公差的等差数列.
∴Sn=25n+
=-
n2+
n.
∵n∈N*,
∴当n=15时,(Sn)max=
.
故选:C.
an+1=an-
| 7 |
| 4 |
| 7 |
| 4 |
∴数列{an}是以a1=25为首项,以-
| 7 |
| 4 |
∴Sn=25n+
n(n-1)×(-
| ||
| 2 |
| 7 |
| 8 |
| 207 |
| 8 |
∵n∈N*,
∴当n=15时,(Sn)max=
| 765 |
| 4 |
故选:C.
点评:本题考查了数列递推式,考查了等差数列的前n项和,训练了二次函数最值的求法,是中档题.

练习册系列答案
相关题目
下列哪个函数的图象只需平移变换即可得到f(x)=sinx+cosx的函数图象( )
A、f1(x)=
| ||||||||
| B、f2(x)=sinx | ||||||||
C、f3(x)=
| ||||||||
D、f4(x)=
|
已知(1+2x)8展开式的二项式系数的最大值为a,系数的最大值为b,则
=( )
| b |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x,y满足不等式组
,则z=2x+2y的最小值为( )
|
A、
| |||||
| B、2 | |||||
C、3
| |||||
D、3
|
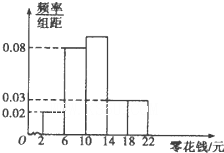 为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为
为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为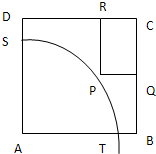 如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧
如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧