题目内容

数列{an}为等比数列，a1=2，且a1，a2+2，a3成等差数列，求an．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用a1=2，且a1，a2+2，a3成等差数列，求出公比，即可求an．
解答： 解：设公比为q，则
∵a1，a2+2，a3成等差数列，
∴2（a2+2）=a1+a3，
∵a1=2，
∴2（2q+2）=2+2q2，
∴q2-2q-1=0，
∴q=1±
2
，
∴an=2•（1±
2
）n-1．
点评：本题考查等差数列的性质，考查等比数列的通项，正确求出公比是关键．
练习册系列答案
相关题目
若三点A（2，3），B（3，4），C（a，b）共线，则有（　　）
A、a=3，b=-5
B、a-b+1=0
C、2a-b=3
D、a-2b=0
为了普及环保知识增强环保意识，某校从理工类专业甲班抽取60人，从文史类乙班抽取50人参加环保知识测试
（1）根据题目条件完成下面2×2列联表，并据此判断你是否有99%的把握认为环保知识与专业有关
优秀 非优秀 总计
甲班
乙班 30
总计 60
（2）为参加上级举办的环保知识竞赛，学校举办预选赛，预选赛答卷满分100分，优秀的同学得60分以上通过预选，非优秀的同学得80分以上通过预选，若每位同学得60分以上的概率为
1
2
，得80分以上的概率为
1
3
，现已知甲班有3人参加预选赛，其中1人为优秀学生，若随机变量X表示甲班通过预选的人数，求X的分布列及期望E（X）．附：k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，n=a+b+c+d
P（K2＞k0） 0.100 0.050 0.025 0.010 0.005
k0 2.706 3.841 5.024 6.635 7.879
在数列{an}中，若an2-an-12=k（n≥2，n∈N*，k为常数），则称{an}为X数列．
（Ⅰ）若数列{bn}是X数列，b1=1，b2=3，写出所有满足条件的数列{bn}的前4项；
（Ⅱ）证明：一个等比数列为X数列的充要条件是公比为1或-1；
（Ⅲ）若X数列{cn}满足c1=2，c2=2
2
，cn＞0，设数列{
1
cn
}的前n项和为Tn．是否存在正整数p，q，使不等式Tn＞
pn+q
-1对一切n∈N*都成立？若存在，求出P，q的值；若不存在，说明理由．
已知函数f（x）=ex，g（x）=ax2（a∈R，a≠0）．
（1）求函数y=
g(x)
f(x)
的单调区间；
（2）①已知A（x1，y1），B（x2，y2）（x1＜x2）为函数y=g（x）图象上的两点，y=g′（x）为y=g（x）的导函数，若g′（x0）=
y1-y2
x1-x2
，求证：x0∈（x1，x2）；
②类比函数y=g（x），①中的结论在函数y=f（x）中是否成立？若成立，请给出证明；若不成立，请说明理由．
如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC=CD，过C作圆O的切线交AD于E．若AB=10，ED=3，求BC的长．
已知f（x）=cos（2x+
π
3
）+1-2cos2x．
（1）求函数f（x）的单调递减区间；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，且a=1，b+c=2，f（A）=-
1
2
，求△ABC的面积．
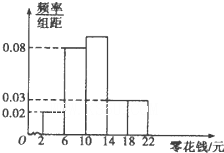为了引导学生树立正确的消费观，某校调查了全校1000名学生每天零花钱的数量，绘制频率分布直方图如图，则每天的零花钱数量在[6，14）内的学生人数为
 
．
数列{an}中，a1，a2，a3成等差数列，a2，a3，a4成等比数列，a3，a4，a5的倒数成等差数列，则a1，a3，a5成
 
数列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网