题目内容
设x,y为正实数,下列命题:
①若x2-y2=1,则x-y<1;
②若
-
=1,则x-y<1;
③若
-
=1,则x-y<1.
其中的真命题有 .(写出所有真命题的编号)
①若x2-y2=1,则x-y<1;
②若
| 1 |
| y |
| 1 |
| x |
③若
| x |
| y |
其中的真命题有
考点:不等式的基本性质
专题:不等式的解法及应用
分析:利用不等式的性质即可得出.
解答:
解:①∵x,y为正实数,∴x-y<x+y,
∵x2-y2=(x-y)(x+y)=1,
∴(x-y)2<1,∴x-y<1,因此正确;
②∵
-
=1,∴x-y=xy,
取x=2,y=
,则x-y>1,因此不正确;
③∵
-
=1,取y=1,x=4,则x-y>1,因此不正确.
综上可知:只有①正确.
故答案为:①.
∵x2-y2=(x-y)(x+y)=1,
∴(x-y)2<1,∴x-y<1,因此正确;
②∵
| 1 |
| y |
| 1 |
| x |
取x=2,y=
| 2 |
| 3 |
③∵
| x |
| y |
综上可知:只有①正确.
故答案为:①.
点评:本题考查了不等式的性质,属于基础题.

练习册系列答案
相关题目
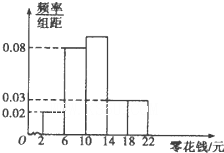 为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为
为了引导学生树立正确的消费观,某校调查了全校1000名学生每天零花钱的数量,绘制频率分布直方图如图,则每天的零花钱数量在[6,14)内的学生人数为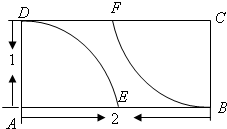 如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是