题目内容
已知y=
+2
，则y的最大值是 ．
| 3-x |
| x-1 |
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：通过对函数求导找出单调区间，从而求出最值．
解答：
解：∵3-x≥0，x-1≥0，
∴定义域为：[1，3]，
∵y′=
-
=
，
令分子为0，解得：x=
，
在（1，
）上，y是增函数，
在（
，3）上，y是减函数；
∴当x=
时，y最大，
ymax=
+2
=
．
故答案为：
．
∴定义域为：[1，3]，
∵y′=
| 1 | ||
|
| 1 | ||
2
|
2
| ||||
2
|
令分子为0，解得：x=
| 13 |
| 5 |
在（1，
| 13 |
| 5 |
在（
| 13 |
| 5 |
∴当x=
| 13 |
| 5 |
ymax=
3-
|
|
| 10 |
故答案为：
| 10 |
点评：本题是求函数的最值问题，通过导数求最值是方法之一，本题是一道基础题．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
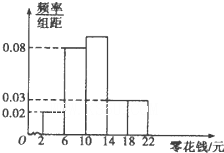为了引导学生树立正确的消费观，某校调查了全校1000名学生每天零花钱的数量，绘制频率分布直方图如图，则每天的零花钱数量在[6，14）内的学生人数为
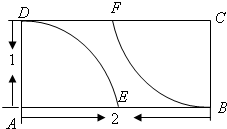如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF（该矩形区域内无其他信号来源，基站工作正常）．若在该矩形区域内随机地选一地点，则该地点无信号的概率是下列哪个函数的图象只需平移变换即可得到f（x）=sinx+cosx的函数图象（ ）
A、f1（x）=
| ||||||||
| B、f2（x）=sinx | ||||||||
C、f3（x）=
| ||||||||
D、f4（x）=
|