题目内容
《张丘建算经》卷上第22题--“女子织布”问题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:设该妇子织布每天增加d尺,由等差数列的前n项和公式能求出结果.
解答:
解:设该妇子织布每天增加d尺,
由题意知S30=30×5+
d=390,
解得d=
.
故该女子织布每天增加
尺.
故选:B.
由题意知S30=30×5+
| 30×29 |
| 2 |
解得d=
| 16 |
| 29 |
故该女子织布每天增加
| 16 |
| 29 |
故选:B.
点评:本题考查等差数列的公差的求法,是基础题,解题时要认真审题,注意等差数列的前n项和公式的合理运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知向量
,
,
满足|
|=4,|
|=2
,
与
的夹角为
,(
-
)•(
-
)=-1,则|
-
|的最大值为( )
| a |
| b |
| c |
| a |
| b |
| 2 |
| a |
| b |
| π |
| 4 |
| c |
| a |
| c |
| b |
| c |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列哪个函数的图象只需平移变换即可得到f(x)=sinx+cosx的函数图象( )
A、f1(x)=
| ||||||||
| B、f2(x)=sinx | ||||||||
C、f3(x)=
| ||||||||
D、f4(x)=
|
已知变量x,y满足不等式组
,则z=2x+2y的最小值为( )
|
A、
| |||||
| B、2 | |||||
C、3
| |||||
D、3
|
 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=10,ED=3,求BC的长.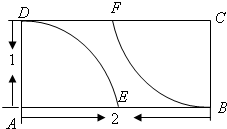 如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是