题目内容
20．给出下列命题，其中正确的个数是（ ）①空集没有子集；
②空集是任何一个集合的真子集；
③任何一个集合都有两个或两个以上的子集；
④若集合B⊆A，则若元素不属于A，则必不属于B．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 利用任何一个集合是它本身的子集，空集是任何一个非空集合的真子集，及其集合的性质即可判断出．
解答 解：①空集是它本身的子集，因此不正确；
②空集是任何一个非空集合的真子集，因此不正确；
③任何一个集合都有两个或两个以上的子集，空集只有一个子集，是它本身，因此不正确；
④若集合B⊆A，则若元素不属于A，则一定不属于B，因此正确．
综上只有④正确．
故选：A．
点评 本题考查了集合的运算及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
15．设圆C：x2+y2-2x-2y-m=0与直线y=x-4相切，则圆C的半径为（ ）
| A． | 2$\sqrt{2}-2$ | B． | 10 | C． | 6 | D． | 2$\sqrt{2}$ |
9．
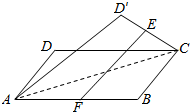设E，F分别是正方形ABCD中CD、AB边的中点，将△ADC沿对角线AC对折，使得直线EF与AC异面，记直线EF与平面ABC所成角为α，与异面直线AC所成角为β，则当tanβ=$\frac{1}{2}$时，tanα=（ ）
设E，F分别是正方形ABCD中CD、AB边的中点，将△ADC沿对角线AC对折，使得直线EF与AC异面，记直线EF与平面ABC所成角为α，与异面直线AC所成角为β，则当tanβ=$\frac{1}{2}$时，tanα=（ ）| A． | $\frac{3\sqrt{5}}{16}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{\sqrt{51}}{17}$ | D． | $\frac{\sqrt{57}}{19}$ |
10．在梯形ABCD中，AB∥CD，$\overrightarrow{AB}$=2$\overrightarrow{DC}$，$\overrightarrow{BE}$=$\overrightarrow{EC}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则向量$\overrightarrow{AE}$等于（ ）
| A． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B． | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |