题目内容
8.已知数列{an}中,a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{a_n}-2,({a_n}>2)\\-{a_n}+3,({a_n}≤2)\end{array}$(n∈N*),记Sn=a1+a2+…+an,若Sn=2015,则n=1343.分析 a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{a_n}-2,({a_n}>2)\\-{a_n}+3,({a_n}≤2)\end{array}$(n∈N*),可得a2=-a1+3=3-a∈[1,3).对a分类讨论:①当a∈[1,2]时,3-a∈[1,2],∴a3=-a2+3=a,….②当a∈(0,1)时,3-a∈(2,3),可得a3=a2-2=1-a∈(0,1),∴a4=-a3+3=a+2∈(2,3),a5=a4-2,对n分类讨论即可得出.
解答 解:∵a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{a_n}-2,({a_n}>2)\\-{a_n}+3,({a_n}≤2)\end{array}$(n∈N*),
∴a2=-a1+3=3-a∈[1,3).
①当a∈[1,2]时,3-a∈[1,2],∴a3=-a2+3=a,….
∴当n=2k-1,k∈N*时,a1+a2=a+3-a=3,∴S2k-1=3(k-1)+a=2015,a=1时舍去,a=2时,k=672,此时n=1343;
当n=2k,k∈N*时,a1+a2=a+3-a=3,∴S2k=3k=2015,k=671+$\frac{2}{3}$,不是整数,舍去;
②当a∈(0,1)时,3-a∈(2,3),∴a3=a2-2=1-a∈(0,1),∴a4=-a3+3=a+2∈(2,3),a5=a4-2=a∈(2,3),….
当n=4k,k∈N*时,a1+a2+a3+a4=a+3-a+1-a+a+2=6,∴S4k=6k=2015,k不为整数,舍去;
当n=4k-1,k∈N*时,a1+a2+a3=a+3-a+1-a=4-a,∴S4k-1=6(k-1)+(4-a)=2015,舍去;
当n=4k-2,k∈N*时,a1+a2=3,∴S4k-2=6(k-1)+3=2015,舍去.
当4k-3,k∈N*时,∴S4k-2=6(k-1)+a=2015,舍去.
综上可得:n=1343.
故答案为:1343.
点评 本题考查了分段数列的性质、分类讨论方法,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案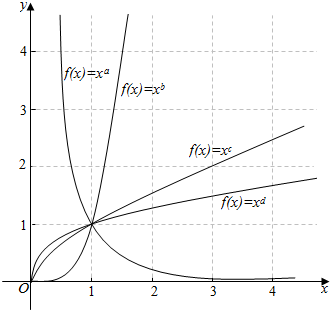
| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ 或 $\frac{2π}{3}$ |
| A. | 0 | B. | 4 | C. | 12 | D. | 10 |
①空集没有子集;
②空集是任何一个集合的真子集;
③任何一个集合都有两个或两个以上的子集;
④若集合B⊆A,则若元素不属于A,则必不属于B.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
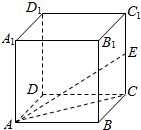
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |