题目内容
9.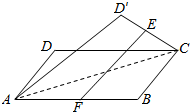 设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )
设E,F分别是正方形ABCD中CD、AB边的中点,将△ADC沿对角线AC对折,使得直线EF与AC异面,记直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$时,tanα=( )| A. | $\frac{3\sqrt{5}}{16}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{51}}{17}$ | D. | $\frac{\sqrt{57}}{19}$ |
分析 连结AC、BD,交于点O,以O为原点,OB为x轴,OC为y轴,过O作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出tanα.
解答 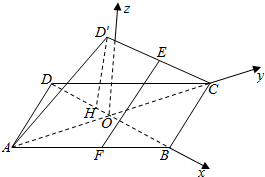 解:连结AC、BD,交于点O,以O为原点,OB为x轴,OC为y轴,过O作平面ABCD的垂线为z轴,建立空间直角坐标系,
解:连结AC、BD,交于点O,以O为原点,OB为x轴,OC为y轴,过O作平面ABCD的垂线为z轴,建立空间直角坐标系,
过D′H⊥平面ABCD,交BD于H,设正方形ABCD边长为2,设OH=a,
则OD=OA=OC=$\sqrt{2}$,D′H=$\sqrt{2-{a}^{2}}$,
则A(0,-$\sqrt{2}$,0),B($\sqrt{2},0,0$),C(0,$\sqrt{2}$,0),D′(-a,0,$\sqrt{2-{a}^{2}}$),
E(-$\frac{a}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2-{a}^{2}}}{2}$),F($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$,0),
$\overrightarrow{AC}$=(0,2$\sqrt{2}$,0),$\overrightarrow{EF}$=($\frac{\sqrt{2}-a}{2}$,-$\sqrt{2}$,-$\frac{\sqrt{2-{a}^{2}}}{2}$),
∵直线EF与平面ABC所成角为α,与异面直线AC所成角为β,则当tanβ=$\frac{1}{2}$,
∴cosβ=$\frac{|\overrightarrow{AC}•\overrightarrow{EF}|}{|\overrightarrow{AC}|•|\overrightarrow{EF}|}$=$\frac{4}{2\sqrt{2}•\sqrt{3-\frac{\sqrt{2}}{2}a}}$=$\frac{2}{\sqrt{5}}$,解得a=$\frac{\sqrt{2}}{2}$,
∴$\overrightarrow{EF}$=($\frac{\sqrt{2}}{4}$,-$\sqrt{2}$,-$\frac{\sqrt{6}}{4}$),
∵平面ABC的法向量$\overrightarrow{n}$=(0,0,1),
∴sinα=$\frac{|\overrightarrow{n}•\overrightarrow{EF}|}{|\overrightarrow{n}|•|\overrightarrow{EF}|}$=$\frac{|-\frac{\sqrt{6}}{4}|}{\sqrt{\frac{5}{2}}}$=$\frac{\sqrt{3}}{2\sqrt{5}}$,
∴tanα=$\frac{\sqrt{51}}{17}$.
故选:C.
点评 本题考查空间角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案①空集没有子集;
②空集是任何一个集合的真子集;
③任何一个集合都有两个或两个以上的子集;
④若集合B⊆A,则若元素不属于A,则必不属于B.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |
| A. | f(2)<f(-$\frac{3}{2}$)<f(-1) | B. | f(-$\frac{3}{2}$)<f(-1)<f(2) | C. | f(2)<f(-1)<f(-$\frac{3}{2}$) | D. | f(2)<f(-$\frac{3}{2}$)<f(-1) |