题目内容
11.对于函数f(x),若存在常数a≠0,使得x取定义域内的每一个值,都有f(x)=-f(2a-x),则称f(x)为“准奇函数”.给定下列函数:①f(x)=$\frac{1}{x+1}$,②f(x)=(x+1)2;③f(x)=x3;④f(x)=sin(x+1),其中的“准奇函数”是①④(写出所有“准奇函数”的序号)分析 判断对于函数f(x)为准奇函数的主要标准是:若存在常数a≠0,函数f(x)的图象关于(a,0)对称,则称f(x)为准奇函数.
解答 解:对于函数f(x),若存在常数a≠0,使得x取定义域内的每一个值,
都有f(x)=-f(2a-x)知,函数f(x)的图象关于(a,0)对称,
对于①:f(x)=$\frac{1}{x+1}$,函数f(x)的图象关于(-1,0)对称,
对于②:f(x)=(x+1)2,函数无对称中心,
对于③:f(x)=x3,函数f(x)关于(0,0)对称,
对于④:f(x)=cosx,函数f(x)的图象关于(kπ,0)对称,
故答案为:①④.
点评 本题考查新定义的理解和应用,函数f(x)的图象关于(a,0)对称,则称f(x)为准奇函数是关键,属于基础题.

练习册系列答案
相关题目
2.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),右焦点F到渐近线的距离为2,F到原点的距离为3,则双曲线C的离心率e为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
16.如图示中的幂函数在第一象限的图象,则下面四个选项中正确的是( )
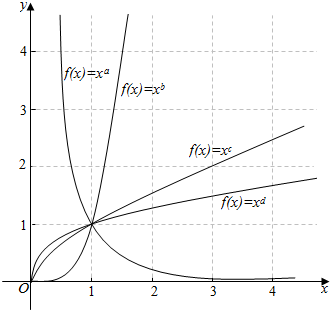

| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
3.在空间四边形ABCD中,CD=2$\sqrt{3}$,AB=2,EF=1,E、F分别是BC、AD的中点,则EF、AB所成的角( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ 或 $\frac{2π}{3}$ |