题目内容
12．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x+2（x＜0）}\\{\sqrt{x}（x≥0）}\end{array}\right.$，若对任意n∈N*，f（f（f…f（a）））=a（n个f），则实数a的个数是（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 ①假设f（a）=a，当a≥0时，则$\sqrt{a}$=a，解得a=1或0；当a＜0时，则a2+4a+2=a，解得a=-1或-2．
②假设f（f（a））=a，对a分类讨论，以此类推即可得出．
解答 解：①假设f（a）=a，当a≥0时，则$\sqrt{a}$=a，解得a=1或0；当a＜0时，则a2+4a+2=a，解得a=-1或-2．
②假设f（f（a））=a，当a≥0时，则f（a）=$\sqrt{a}$，f（f（a））=f（$\sqrt{a}$）=$\sqrt{\sqrt{a}}$，∴$\sqrt{\sqrt{a}}$=a，解得a=1或0；以此类推：当a≥0时，a=1或0．
当a＜0时，则f（a）=a2+4a+2，f（f（a））=（a2+4a+2）2+4（a2+4a+2）+2=a，∴a2+4a+2=a，解得a=-1或-2．以此类推：当a＜0时，
a=-1或-2．
综上可得：实数a的个数是4．
故选：C．
点评 本题考查了一元二次方程的解法、复合函数的性质的性质，考查了分类讨论方法、推理能力与计算能力，属于中档题．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
2．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0），右焦点F到渐近线的距离为2，F到原点的距离为3，则双曲线C的离心率e为（ ）
| A． | $\frac{{\sqrt{5}}}{3}$ | B． | $\frac{{3\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{{\sqrt{6}}}{2}$ |
3．在空间四边形ABCD中，CD=2$\sqrt{3}$，AB=2，EF=1，E、F分别是BC、AD的中点，则EF、AB所成的角（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ 或 $\frac{2π}{3}$ |
20．给出下列命题，其中正确的个数是（ ）
①空集没有子集；
②空集是任何一个集合的真子集；
③任何一个集合都有两个或两个以上的子集；
④若集合B⊆A，则若元素不属于A，则必不属于B．
①空集没有子集；
②空集是任何一个集合的真子集；
③任何一个集合都有两个或两个以上的子集；
④若集合B⊆A，则若元素不属于A，则必不属于B．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
7．若平面α内有无数条直线与平面β平行，则α与β的位置关系是（ ）
| A． | 平行 | B． | 相交 | C． | 平行或相交 | D． | 重合 |
17．如图，在正方体ABCD-A1B1C1D1中，E为CC1的中点，则直线AE与平面ABCD所成角的正切值为（ ）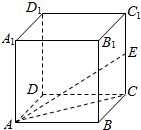
| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | 2$\sqrt{2}$ |
4．若偶函数f（x）在[1，+∞）上是减函数，则下列关系式中成立的是（ ）
| A． | f（2）＜f（-$\frac{3}{2}$）＜f（-1） | B． | f（-$\frac{3}{2}$）＜f（-1）＜f（2） | C． | f（2）＜f（-1）＜f（-$\frac{3}{2}$） | D． | f（2）＜f（-$\frac{3}{2}$）＜f（-1） |