题目内容
5.△ABC中,角A、B、C所对的边分别为a、b、c,a>b且sin2B+sin2C=tan$\frac{A}{2}$(cos2B+cos2C).(I)求角A的大小;
(Ⅱ)若a=4,求b+c的取值范围.
分析 (Ⅰ)通过和差化积公式,三角函数恒等变换的应用化简得tan$\frac{A}{2}$=$\sqrt{3}$,利用正切函数的图象和性质求出A的值.
(Ⅱ)通过余弦定理以及基本不等式求出b+c的范围,再利用三角形三边的关系求出b+c的范围.
解答 解:(I)∵sin2B+sin2C=tan$\frac{A}{2}$(cos2B+cos2C).
∴2sin(B+C)cos(B-C)=2tan$\frac{A}{2}$cos(B+C)cos(B-C),
∴sinAcos(B-C)=-tan$\frac{A}{2}$cosAcos(B-C),
∴可得:sinA=-tan$\frac{A}{2}$cosA,
∴可得:tanA=$\frac{2tan\frac{A}{2}}{1-ta{n}^{2}\frac{A}{2}}$=-tan$\frac{A}{2}$,解得:tan$\frac{A}{2}$=$\sqrt{3}$,
∴由$\frac{A}{2}$∈(0,$\frac{π}{2}$)解得:A=$\frac{2π}{3}$.
(Ⅱ)由余弦定理得,a2=b2+c2-2bccosA,
则16=b2+c2+bc,
∴(b+c)2-bc=16,
即bc=(b+c)2-16≤[$\frac{1}{2}$(b+c)]2,
化简得,(b+c)2≤$\frac{64}{3}$(当且仅当b=c时取等号),
则b+c≤$\frac{8\sqrt{3}}{3}$,又b+c>a=4,
综上得,b+c的取值范围是(4,$\frac{8\sqrt{3}}{3}$].
点评 本题考查余弦定理的应用,和差化积公式,三角函数恒等变换的应用以及基本不等式求最值,考查分析问题、解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知集合M={x|-$\sqrt{5}$<x<$\sqrt{3}$,x∈Z},则下列集合是集合M的子集的为( )
| A. | P={-3,0,1} | B. | Q={-1,0,1,2} | C. | R={y|-π<y<-1,y∈Z} | D. | S={x||x|≤$\sqrt{3}$,x∈N} |
16.如图示中的幂函数在第一象限的图象,则下面四个选项中正确的是( )
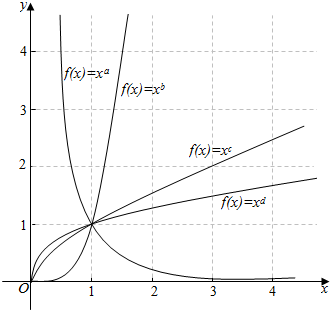

| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
13.已知圆Г过点(1,1)、(1,3)、(2,2),P是圆Г的一个动点,若A(-3,4),O为坐标原点,则$\overrightarrow{OP}$•$\overrightarrow{OA}$的最大值为( )
| A. | 0 | B. | 4 | C. | 12 | D. | 10 |
20.给出下列命题,其中正确的个数是( )
①空集没有子集;
②空集是任何一个集合的真子集;
③任何一个集合都有两个或两个以上的子集;
④若集合B⊆A,则若元素不属于A,则必不属于B.
①空集没有子集;
②空集是任何一个集合的真子集;
③任何一个集合都有两个或两个以上的子集;
④若集合B⊆A,则若元素不属于A,则必不属于B.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.如图,在正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线AE与平面ABCD所成角的正切值为( )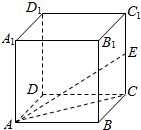

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |
15.若x>0,则下面式子中最小值等于6的是( )
| A. | x+$\frac{16}{x}$ | B. | x2+$\frac{16}{x}$ | C. | x+$\frac{32}{{x}^{2}}$ | D. | x+$\frac{36}{x}$ |